Свойства степенных рядов.

Степенным рядом называется функциональный ряд вида ,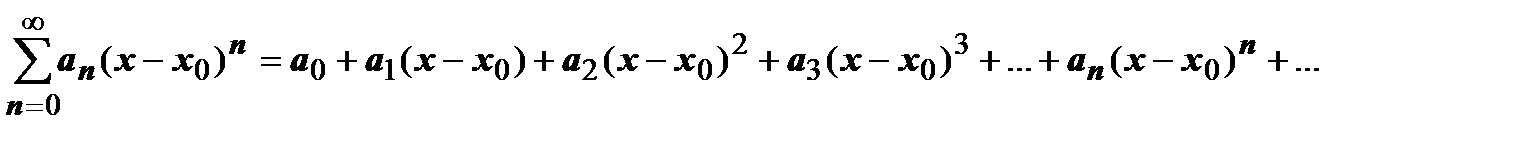

где 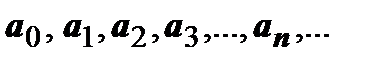- постоянные (коэффициенты ряда), 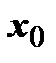- фиксированное число (центр сходимости). Степенной ряд имеет по меньшей мере одну точку сходимости - точку .

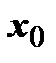Почленное интегрирование или дифференцирование степенного ряда не меняют его радиус сходимости.

Доказательство. Под почленным интегрированием понимается интегрирование ряда 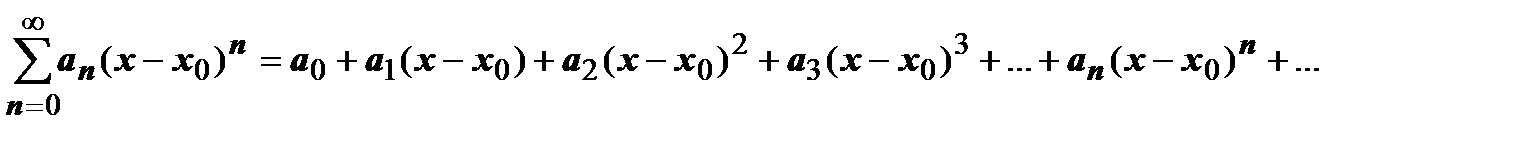по отрезку 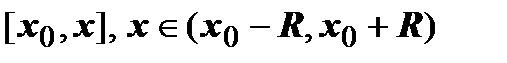. Результат этой операции: .

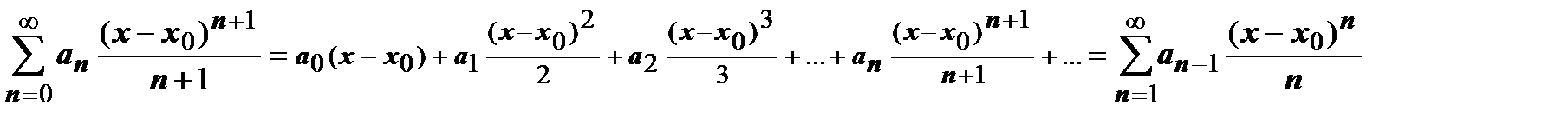Это тоже степенной ряд, его радиус сходимости 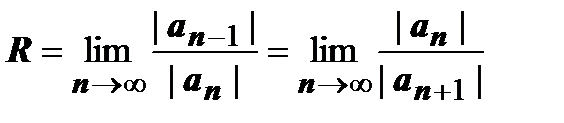равен радиусу сходимости исходного ряда.

Ряд, получающийся в результате почленного дифференцирования тоже степенной ряд: 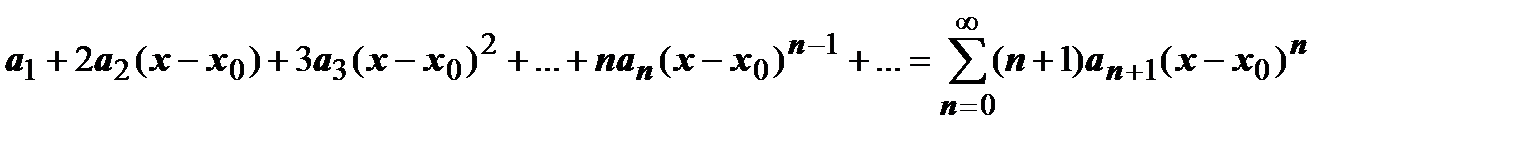. Его радиус сходимости 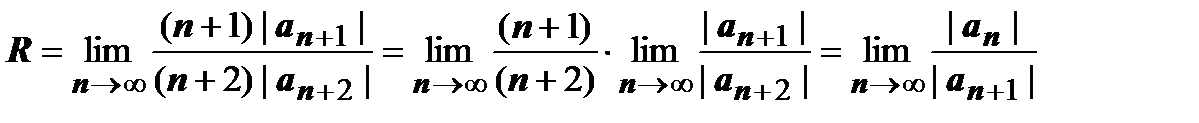тоже равен радиусу сходимости исходного ряда.

2. (Почленное интегрирование степенного ряда). Пусть сумма степенного ряда на области сходимости равна функции 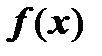, т.е. 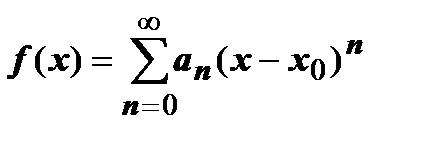. Тогда для .

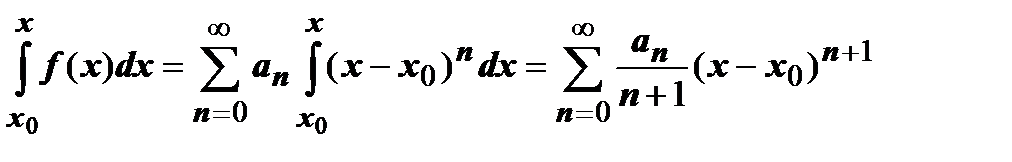Доказательство. Справедливость этого утверждения следует из равномерной сходимости степенного ряда на отрезке иТеоремы 18.2.3.2 о почленном интегрировании равномерно сходящегося ряда.

3. (Почленное дифференцирование степенного ряда). Степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и .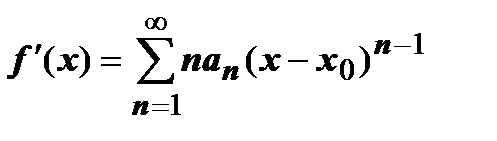

Доказательство. Справедливость этого утверждения следует из равномерной сходимости степенного ряда, составленного из производных членов исходного ряда, на любом отрезке, лежащем в интервале сходимости иТеоремы 18.2.3.3 о почленном дифференцировании равномерно сходящегося ряда.

4. (Бесконечная дифференцируемость суммы степенного ряда). Сумма 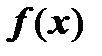степенного ряда в любой точке интервала сходимости имеет производные любого порядка; эти производные могут быть получены последовательным почленным дифференцированием исходного ряда.

Доказательство. Справедливость этого утверждения следует из доказанной теоремы о почленном дифференцировании степенного ряда; последовательное применение этой теоремы даёт 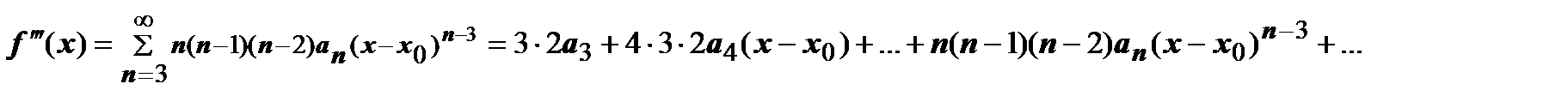и т.д.

4. Расставить пределы интегрирования, поменять порядок, перейти к полярным.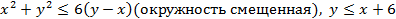

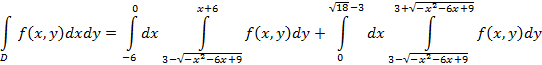
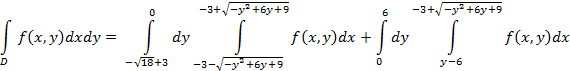
5. Момент инерции относительно начала координат, Поверхностная плотность

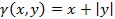
r wsp: rsidR=" 00000000" > < w: pgSz w: w=" 12240" w: h=" 15840" /> < w: pgMar w: top=" 1134" w: right=" 850" w: bottom=" 1134" w: left=" 1701" w: header=" 720" w: footer=" 720" w: gutter=" 0" /> < w: cols w: space=" 720" /> < /w: sectPr> < /w: body> < /w: wordDocument> ">

6. Исследовать на сходимость

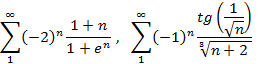
1)

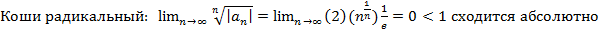
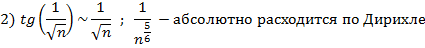
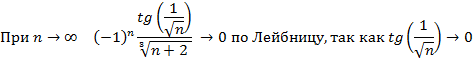
Билет №15

1. Тройной интеграл и его свойства.

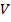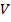Пусть в замкнутой области пространства задана непрерывная функция . Разбив область сеткой поверхностей на частей и выбрав в каждой из них произвольную точку 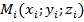, составим интегральную сумму 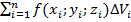для функции

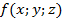по области .

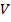Если предел интегральной суммы существует при неограниченном увеличении числа таким образом, что каждая «элементарная область» 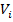стягивается в точку (т.е. диаметр области стремится к нулю), то его называют тройным интегралом от функции по области 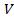и обозначают:

Свойства:

1. Линейность

> .

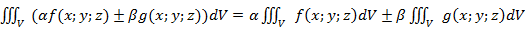2. Аддитивность

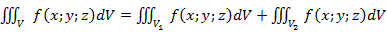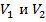, если , а пересечение состоит из границы, их разделяющей.

3. Теорема об оценке

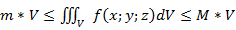, где 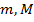- соответственно наименьшее и наибольшее значения функции 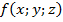в области .

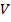4. Теорема о среднем значении

Если функция 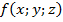непрерывна в замкнутой области 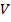, то в этой области существует такая точка 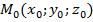, что

где 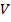- объем тела.

5. Монотонность

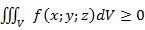, если в области 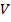функция 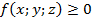. Если в области интегрирования 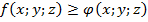, то и .

6. Интеграл от единичной функции равен объёму тела

2. Операторы Гамильтона и Лапласа. Основные операции. Дифференциальные операции второго порядка.

Основные дифференциальные операции над скалярным полем 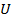и векторным 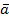являются 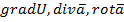и они называются векторными операциями первого порядка.

Эти операции удобно записывать с помощью оператора Гамильтона

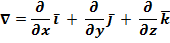
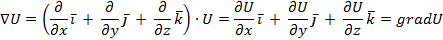
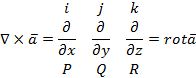
После применения оператора Гамильтона к скалярному или векторному полю получается новое поле, к которому можно применить этот оператор. Получаются дифференциальные операции второго порядка.

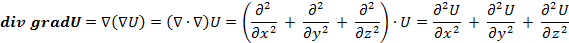
Правая часть этого равенства называется оператором Лапласа скалярной функции 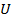и обозначается 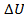. Решениями уравнения Лапласа являются гармонические функции.

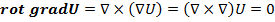
Так как векторное произведение двух одинаковых векторов равно нулю. Это означает, что поле градиента есть поле безвихревое.

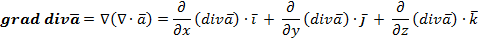
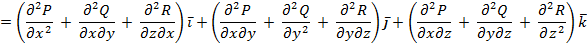
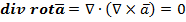
Так как смешанное произведение трех векторов, из которых два одинаковые, равно нулю. Это означает, что поле вихря соленоидальное.

Так как двойное векторное произведение обладает свойством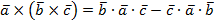

Здесь 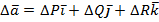– векторная величина, полученнаяя в результате применения оператора Лапласа к вектору .

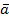3. Интегральный признак сходимости знакоположительных рядов.

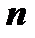
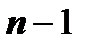
х

у

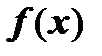
Теорема. Пусть члены положительного числового ряда являются значениями непрерывной монотонно убывающей неотрицательной функции 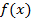при натуральных значениях аргумента: Тогда ряд и несобственный интеграл сходятся или расходятся одновременно.

Доказательство. Обозначим. 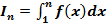. Согласно геометрическому смыслу определённого интеграла, это площадь криволинейной трапеции под кривой над отрезком [1, n ]. Частичная сумма 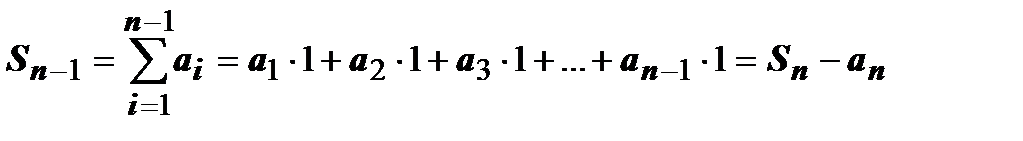- площадь ступенчатой фигуры, расположенной над криволинейной трапецией (сплошная верхняя граница на рисунке). Сумма 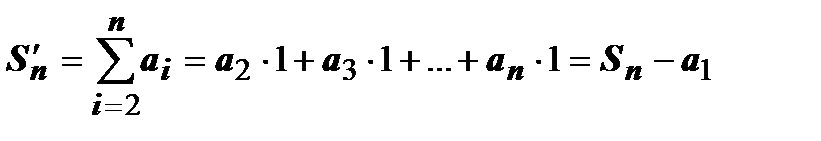- площадь ступенчатой фигуры, расположенной под криволинейной трапецией (пунктирная верхняя граница на рисунке). Очевидно, 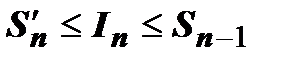, или . Из этого неравенства, в котором 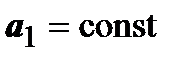, , 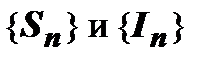- монотонно возрастающие с ростом n последовательности, и следуют все утверждения теоремы. Например:

1. Пусть интеграл сходится. Это означает, что существует конечный , т.е. последовательность ограничена сверху 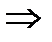последовательность 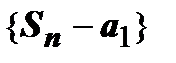ограничена сверху 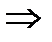существует конечный 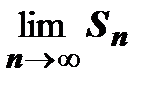, т.е. ряд сходится.

2. Пусть интеграл расходится. Это означает, что бесконечен, т.е. последовательность неограничена сверху 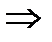последовательность неограничена сверху 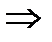не существует конечного 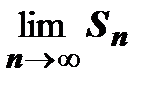, т.е. ряд расходится.

4. Вычислить криволинейный интеграл двумя способами .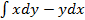

Проверяем что интеграл не зависит от пути интегрирования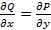

1 способ через формулу Грина

по площади.

2 способ в лоб по пути от точки О до А и до Б

5. Вычислить массу поверхности полусферы 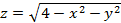, вырезанной цилиндром 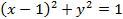, если плотность оболочки полусферы .

 

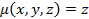⇐ Предыдущая45678910111213Следующая ⇒

Поделиться с друзьями: