В соленоидальном поле поток вектора через поперечное сечение векторной трубки сохраниет своё постоянное значение.

Рассмотрим векторную трубку между двумя её произвольными сечениями S­₁ и S₃; боковую поверхность обозначим S­₃. Поток вектора через замкнутую поверхность, состоящую из S­₁, S­₂ и S­_3­, равен нулю.

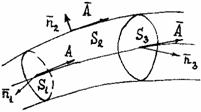
Следовательно

где – внешняя нормаль.

Так как на боковой поверхности векторной трубки нормаль перпендикулярна к векторам поля, то . Тогда

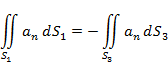
Поменяв направление нормали на площадке , т.е. взяв внутреннюю нормаль 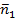, получим:

2. Вычисление площади поверхности с помощью двойного интеграла

Предположим, что поверхность задаётся неявным уравнением ( 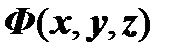- непрерывно дифференцируемая функция) и взаимно однозначно проецируется в область на плоскости Оху. Из теории функций нескольких переменных известно, что градиент функции ортогонален поверхности уровня этой функции, проходящей через точку, в которой найден градиент. Рассматривая уравнение как уравнение поверхности уровня функции трёх переменных , получаем, что в каждой точке поверхности ортогонален , т.е. является нормальным к вектором. Чтобы получить единичный нормальный вектор, достаточно просто пронормировать : , где знак перед дробью соответствует возможности выбора двух возможных взаимно противоположных направлений нормали. В координатной форме , где 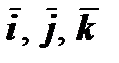- базисные орты. Если сравнить это выражение с представлением градиента через направляющие косинусы: , то , , . Теперь мы можем выразить элемент площади поверхности через элемент площади в каждой координатной плоскости: , , 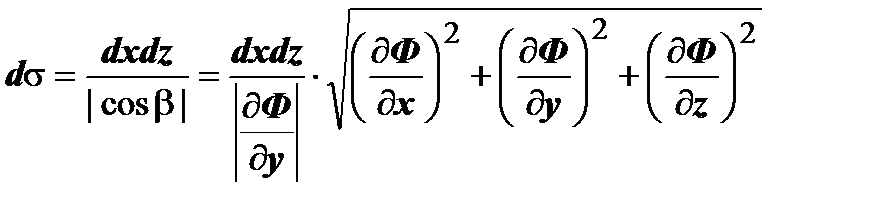. В частном случае задания уравнения поверхности в явном виде получим 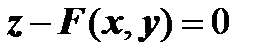, т.е. , , , , 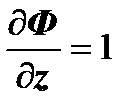поэтому , , , и 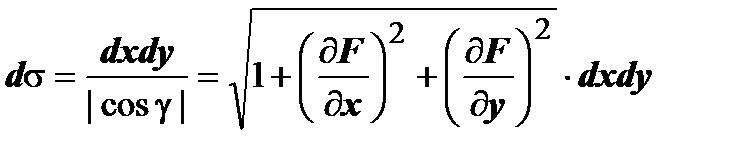.