Студопедия

Главная страница Случайная страница

КАТЕГОРИИ:

АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника






Билет 11.


⇐ ПредыдущаяСтр 5 из 28Следующая ⇒




1 Вопрос) Тройной интеграл в цилиндрических координатах. В этой координатной системе положение точки в пространстве характеризуется тремя числами: r, j и z, где r и j - полярные координаты проекции M1

точки М на плоскость Оху, z - аппликата точки M. Формулы перехода от цилиндрических координат к декартовым:

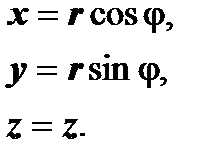
Вычислим якобиан этого преобразования:

 

, следовательно, .

r sin
x
M (x, y, z)= M (r, j, )
z
O
r
j
M1
16.2.5.3. Тройной интеграл в сферических координатах. В этих координатах положение точки M в пространстве характеризуется тремя числами: r, j и , где r - длина радиуса-вектора точки M, j - полярный угол проекции M1 точки М на плоскость Оху, - угол между радиусом-вектором точки M и осью Oz. Формулы перехода от сферических координат к декартовым:

Вычислим якобиан этого преобразования: 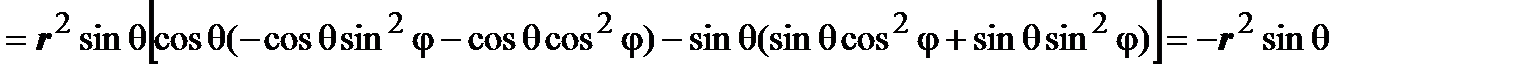, следовательно, .

2 Вопрос) Теорема Остроградского. Пусть - кусочно-гладкая замкнутая поверхность, ограничивающая область V, - гладкое векторное поле. Тогда поток поля через внешнюю сторону равен тройному интегралу от дивергенции поля по V:

.

Приведённую выше формулу обычно называют формулой Остроградского в векторной форме. Если записать её в виде или , то получим формулу Остроградского в координатной форме.

х
у
ху
z
Доказательство. Достаточно доказать формулу в случае, когда тело V - простое, т.е. проекция V на любую координатную плоскость - простая область D, и любая прямая, перпендикулярная этой плоскости и проходящая через внутреннюю точку V, пересекает границу V в двух точках. Если V не является простой областью, мы разобьём её на простые части; тогда сумма тройных интегралов по этим частям, в силу аддитивности, даст интеграл по всей области V; а при вычислении поверхностных интегралов интегралы по введённым внутренним перегородкам будут браться дважды с противоположными направлениями нормали и взаимно уничтожатся. 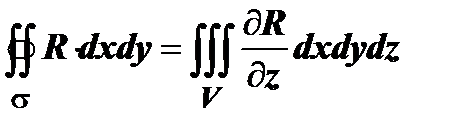Кроме того, достаточно доказать формулу Остроградского для каждого из слагаемых: , , , тогда сумма этих формул даст общую формулу. Докажем, например, что 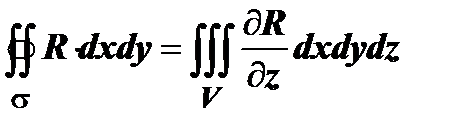. Простую область V, как мы знаем, можно описать следующим образом: . Вычисляем : . 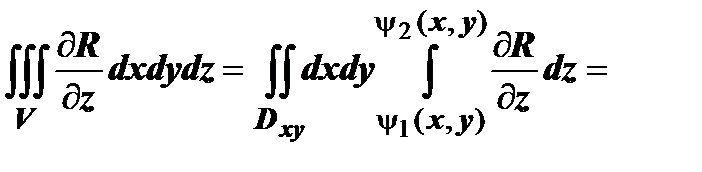Знак последнего слагаемого выбран с учётом того, что на . Если в полной границе области V присутствует цилиндрическая составляющая , то , поэтому окончательно . Совершенно аналогично доказываются формулы для двух других слагаемых. Формула Остроградского доказана.

3 Вопрос) Достаточный признак сходимости знакочередующегося ряда (признак Лейбница). Если

1. Последовательность, составленная из модулей членов знакочередующегося ряда, монотонно убывает, т.е. ;

2. Выполняется необходимый признак сходимости ряда, т.е. ,

то ряд сходится. Его сумма по абсолютной величине не превосходит абсолютную величину первого члена.

 

ПРИМЕР! С помощью признака Лейбница доказывается сходимость рядов , . , и т.д. Третий из этих рядов сходится абсолютно ( сходится), остальные - условно (ряды из модулей членов расходятся


4.Вычислите объём тела ограниченного поверхностями:

Пересечение:

V=

 

 


⇐ Предыдущая12345678910Следующая ⇒
Поделиться с друзьями:
mylektsii.su - Мои Лекции - 2015-2025 год. (0.009 сек.)Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав Пожаловаться на материал