
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Билет 2.
|
|
Билет 1.
Теорема о среднем и об оценке двойного интеграла. доказательство.


Поверхностный интеграл первого рода. способ вычисления. пример.






3. разложение в ряд Тейлора и Маклорена. разложение в ряд маклорена функции y=ex. докозательство.







Задание №4




Задание №5

n=(-3, 0, 0), n0=(-1, 0, 0) (нормировали)
a*n= 5-2x

 x=3)=
x=3)= 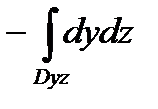 =(интеграл – площадь круга)=
=(интеграл – площадь круга)= 
Задача №6
а)

Лейбниц и признак сравнения:

Ряд 1/n – расходится. => Первоначальный ряд сходится условно и монотонно убывает.
б)

Лейбниц и Даламбер:

ряд расходится. => Исходный ряд условно сходится.
Билет 2.
1. Теорема о среднем и об оценке для тройного интеграла.


Док-во. Непрерывная на ограниченном замкнутом объеме V функция f(P) принимает в некоторых точках этой области свое минимальное m и максимальное M значения. Так как m ≤ f(P) ≤ M, то m·ν (V)≤  ≤ M·ν (V) или
≤ M·ν (V) или  . Непрерывная функция принимает, кроме того, любое значение, заключенное мeжду m и M, в частности, значение
. Непрерывная функция принимает, кроме того, любое значение, заключенное мeжду m и M, в частности, значение  . Следовательно,
. Следовательно,  такое что
такое что  , откуда и следует доказываемо утверждение.
, откуда и следует доказываемо утверждение.


Док-во. 

 m·ν (V)≤
m·ν (V)≤  ≤ M·ν (V)
≤ M·ν (V)
2. Определение криволинейного интеграла второго рода. Способ его вычисления. Пример.



РАВНОМЕРНО СХОДЯЩИЙСЯ РЯД
функциональный ряд

с (вообще говоря) комплексными членами, сходящийся на множестве X, и такой, что для любого ɛ > 0 существует номер nɛ , что для всех n > nɛ и всех выполняется неравенство

где

и

Иными словами, последовательн  ость частичных сумм sin(х).является равномерно сходящейся последовательностью. Определение Р. с. р. равносильно выполнению условия
ость частичных сумм sin(х).является равномерно сходящейся последовательностью. Определение Р. с. р. равносильно выполнению условия

что означает равномерную сходимость к нулю на множестве X последовательности остатков

ряда (1).
Пример. Ряд

равномерно сходится на каждом конечном круге комплексной плоскости и не сходится равномерно на всем множестве С комплексных чисел.
Условие равномерной сходимости ряда (1) на множестве X без использования понятия суммы ряда дает Ноши критерий равномерной сходимости ряда. Достаточное условие равномерной сходимости ряда дается Вейерштрасса признаком.
Ряд 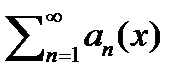 наз. правильно сходящимся на множестве X, если существует такой числовой ряд, что для всех n=1, 2,... и всех
наз. правильно сходящимся на множестве X, если существует такой числовой ряд, что для всех n=1, 2,... и всех  выполняется неравенство
выполняется неравенство

т. е. если ряд (1) удовлетворяет условиям признака Вейерштрасса равномерной сходимости рядов. В силу этого признака правильно сходящийся на множестве X ряд равномерно сходится на этом множестве. Обратное, вообще говоря, неверно; однако во всяком равномерно сходящемся на множестве X ряде можно так объединить следующие друг за другом его члены в конечные группы, что получившийся при этом ряд будет уже правильно сходиться на множестве X.