
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача №6
|
|
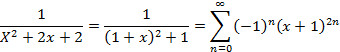
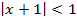
Напоминание

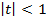
Билет 4
1) Тройной интеграл в цилиндрических координатах. В этой координатной системе положение точки в пространстве характеризуется тремя числами: r, j и z, где r и j - полярные координаты проекции M1
| y |
| x |
| M (x, y, z)= M (r, j, z) |
| z |
| O |
| r |
| j |
| M1 (x, y, 0)= M1 (r, j, 0) |
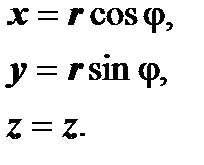
Вычислим якобиан этого преобразования: 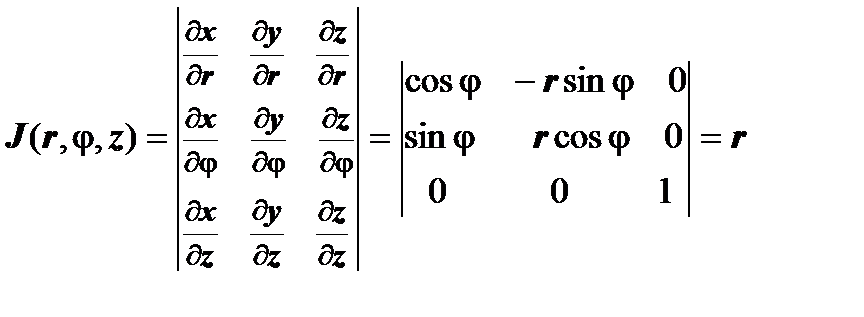 , следовательно,
, следовательно,  .
.
Тройной интеграл в сферических координатах. В этих координатах положение точки M в пространстве характеризуется тремя числами: r, j и  , где r - длина радиуса-вектора точки M, j - полярный угол проекции M1 точки М на плоскость Оху,
, где r - длина радиуса-вектора точки M, j - полярный угол проекции M1 точки М на плоскость Оху,  - угол между радиусом-вектором точки M и осью Oz. Формулы перехода от сферических координат к декартовым:
- угол между радиусом-вектором точки M и осью Oz. Формулы перехода от сферических координат к декартовым:

|
r sin 
|
| x |
M (x, y, z)= M (r, j,  ) )
|
| z |
| O |
| r |
| j |

|
| M1 |

Вычислим якобиан этого преобразования: 

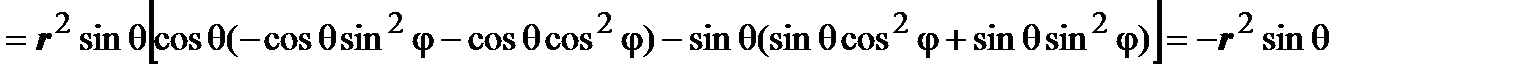 , следовательно,
, следовательно,  .
.
2) Формула Стокса: 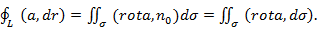 Физический смысл формулы Стокса состоит в том, что циркуляция векторного поля
Физический смысл формулы Стокса состоит в том, что циркуляция векторного поля 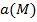 вдоль замкнутого контура
вдоль замкнутого контура  численно равна потоку ротора этого поля через произвольную поверхность
численно равна потоку ротора этого поля через произвольную поверхность  , натянутую на этот контур.
, натянутую на этот контур.
Физический смысл ротора.
Можно использовать представление о вращении брошенной в поток маленькой пылинки (увлекаемой потоком с собой, без его заметного возмущения) или о вращении помещённого в поток с закреплённой осью маленького (без инерции, вращаемого потоком, заметно не искажая его) колеса с прямыми (не винтовыми) лопастями. Если то или другое при взгляде на него вращается против часовой стрелки, то это означает, что вектор ротора поля скорости потока в данной точке имеет положительную проекцию в направлении на нас.
Обычно говорят, что циркуляция характеризует вращательную способность поля. Имеется в виду следующее. Если векторные линии поля замкнуты, то, как мы видели, циркуляция по ним в направлении поля положительна, при этом в гидродинамической интерпретации частицы жидкости крутятся по этим замкнутым линиям. Пусть теперь линии тока произвольны; вообразим в объёме V замкнутый контур С. Если в результате движения жидкости этот контур будет вращаться, то поле обладает вращательной способностью; абсолютная величина циркуляции будет определять угловую скорость вращения (чем больше | Ц |, тем выше скорость); знак циркуляции покажет, совпадает ли направление вращения с направлением интегрирования.
3)
 (-1; 1)
(-1; 1)
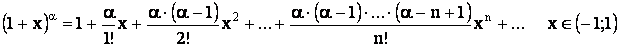
4) Посчитать массу криво. 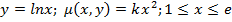
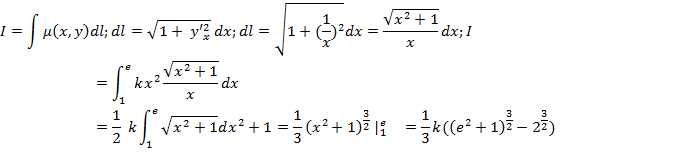
 .
.
5) Посчитать циркуляцию поля с помощью формулы Стокса. Контур 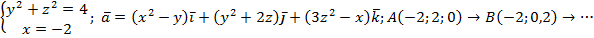
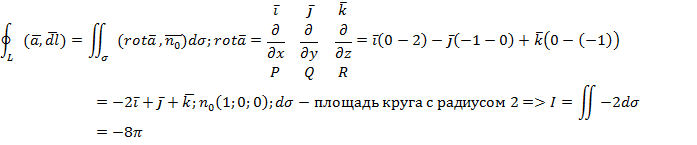
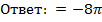
6)
Билет 5
1) Пусть на плоскости Oxy задана ограниченная замкнутая область D с кусочно-гладкой границей, и пусть на области D определена функция  .
.
Разобьём область D произвольным образом на  подобластей
подобластей  (не имеющих общих внутренних точек). Символом
(не имеющих общих внутренних точек). Символом  будем обозначать площадь области
будем обозначать площадь области  ; символом
; символом  здесь и дальше будет обозначаться наибольшее расстояние между двумя точками, принадлежащими области D:
здесь и дальше будет обозначаться наибольшее расстояние между двумя точками, принадлежащими области D:
 ;
;
символом  обозначим наибольший из диаметров областей
обозначим наибольший из диаметров областей  :
:  .
.
В каждой из подобластей  выберем произвольную точку
выберем произвольную точку 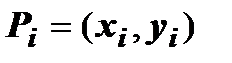 , вычислим в этой точке значение функции
, вычислим в этой точке значение функции  , и составим интегральную сумму
, и составим интегральную сумму  .
.
Если существует предел последовательности интегральных сумм при  , не зависящий ни от способа разбиения области D на подобласти
, не зависящий ни от способа разбиения области D на подобласти  , ни от выбора точек
, ни от выбора точек  , то функция
, то функция  называется интегрируемой по области D, а значение этого предела называется двойным интегралом от функции
называется интегрируемой по области D, а значение этого предела называется двойным интегралом от функции  по области D и обозначается
по области D и обозначается  .
.
| х |
| у |

|

|

|

|
|

|

|

|

|

|
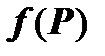 через координаты точки
через координаты точки  , и представить
, и представить  как
как 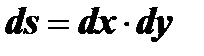 , получим другое обозначение двойного интеграла:
, получим другое обозначение двойного интеграла:  . Это и есть площадь.
. Это и есть площадь.
2) Циркуляцией называется линейный интеграл векторного поля по замкнутой кривой С: 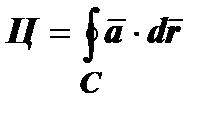 .
.
Обычно говорят, что циркуляция характеризует вращательную способность поля. Имеется в виду следующее. Если векторные линии поля замкнуты, то, как мы видели, циркуляция по ним в направлении поля положительна, при этом в гидродинамической интерпретации частицы жидкости крутятся по этим замкнутым линиям. Пусть теперь линии тока произвольны; вообразим в объёме V замкнутый контур С. Если в результате движения жидкости этот контур будет вращаться, то поле обладает вращательной способностью; абсолютная величина циркуляции будет определять угловую скорость вращения (чем больше | Ц |, тем выше скорость); знак циркуляции покажет, совпадает ли направление вращения с направлением интегрирования.
Ротором векторного поля  (M) в точке
(M) в точке  называется векторная величина (векторное поле)
называется векторная величина (векторное поле)  . Запомнить эту формулу очень легко, если выразить
. Запомнить эту формулу очень легко, если выразить  через оператор Гамильтона набла:
через оператор Гамильтона набла:  равен векторному произведению
равен векторному произведению  . Действительно,
. Действительно,  . Если теперь раскрыть этот определитель по первой строке, получим
. Если теперь раскрыть этот определитель по первой строке, получим
 . Физический смысл ротора. Можно использовать представление о вращении брошенной в поток маленькой пылинки (увлекаемой потоком с собой, без его заметного возмущения) или о вращении помещённого в поток с закреплённой осью маленького (без инерции, вращаемого потоком, заметно не искажая его) колеса с прямыми (не винтовыми) лопастями. Если то или другое при взгляде на него вращается против часовой стрелки, то это означает, что вектор ротора поля скорости потока в данной точке имеет положительную проекцию в направлении на нас.
. Физический смысл ротора. Можно использовать представление о вращении брошенной в поток маленькой пылинки (увлекаемой потоком с собой, без его заметного возмущения) или о вращении помещённого в поток с закреплённой осью маленького (без инерции, вращаемого потоком, заметно не искажая его) колеса с прямыми (не винтовыми) лопастями. Если то или другое при взгляде на него вращается против часовой стрелки, то это означает, что вектор ротора поля скорости потока в данной точке имеет положительную проекцию в направлении на нас.
3) ряд Дирихле (или обобщённый гармонический ряд)
 . (18.3.1)
. (18.3.1)
Если s < 1, то  , и, так как частичные суммы
, и, так как частичные суммы  неограничены, то суммы
неограничены, то суммы  и подавно неограничены, т.е. при s < 1 ряд (18.3.1) расходится. Пусть теперь s > 1. Как и для гармонического ряда сгруппируем члены в частичной сумме по степеням числа 2:
и подавно неограничены, т.е. при s < 1 ряд (18.3.1) расходится. Пусть теперь s > 1. Как и для гармонического ряда сгруппируем члены в частичной сумме по степеням числа 2:  …+
…+  .
.
Структура каждой скобки:  , поэтому
, поэтому  (мы воспользовались формулой для частичной суммы геометрической прогрессии). Последовательность ограничена; ряд сходится.
(мы воспользовались формулой для частичной суммы геометрической прогрессии). Последовательность ограничена; ряд сходится.
Итак, ряд Дирихле (18.3.1) сходится при s > 1, расходится при s 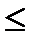 1.
1.
4) Расставьте пределы интегрирования. Перейти к полярным координатам. 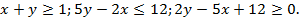
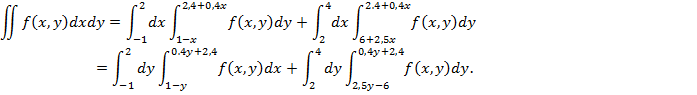
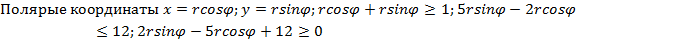
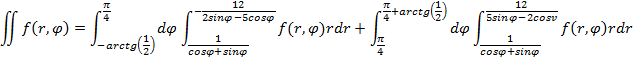
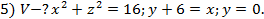

6) а) 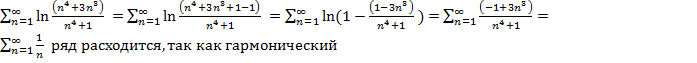
б) 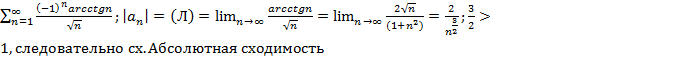

|
| х |
| у |

|

|

|

|

|

|

|
1) Пусть в пространстве Oxyz задана ограниченная замкнутая область (объём) V, и пусть на области V определена функция  .
.
Разобьём область V произвольным образом на  подобластей
подобластей 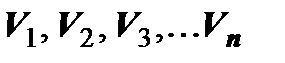 (не имеющих общих внутренних точек). Символом
(не имеющих общих внутренних точек). Символом  будем обозначать объём области
будем обозначать объём области  ; символом
; символом  обозначим наибольший из диаметров областей
обозначим наибольший из диаметров областей 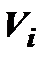 :
:  .
.
В каждой из подобластей  выберем произвольную точку
выберем произвольную точку  , вычислим в этой точке значение функции
, вычислим в этой точке значение функции  , и составим интегральную сумму
, и составим интегральную сумму  .
.
Если существует предел последовательности интегральных сумм при  , не зависящий ни от способа разбиения области V на подобласти
, не зависящий ни от способа разбиения области V на подобласти 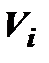 , ни от выбора точек
, ни от выбора точек  , то функция
, то функция  называется интегрируемой по области V, а значение этого предела называется тройным интегралом от функции
называется интегрируемой по области V, а значение этого предела называется тройным интегралом от функции  по области V и обозначается
по области V и обозначается  .
.
Если расписать значение 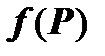 через координаты точки
через координаты точки  , и представить
, и представить  как
как  , получим другое обозначение тройного интеграла:
, получим другое обозначение тройного интеграла:  . Итак, кратко,
. Итак, кратко,  .
.
Линейность. Если функции  ,
,  интегрируемы по области V, то их линейная комбинация
интегрируемы по области V, то их линейная комбинация  тоже интегрируема по
тоже интегрируема по  , и
, и 
 .
.
Аддитивность. Если область  является объединением двух областей
является объединением двух областей  и
и  , не имеющих общих внутренних точек, то
, не имеющих общих внутренних точек, то  .
.
Монотонность. Если в любой точке  выполняется неравенство
выполняется неравенство  , и функции
, и функции  интегрируемы по области V, то
интегрируемы по области V, то  .
.
2) Теорема Стокса. Пусть в пространственной области V задано гладкое векторное поле

|

|

|
 (M) и
(M) и  - незамкнутая кусочно-гладкая поверхность, ограниченная контуром С. Единичный вектор нормали
- незамкнутая кусочно-гладкая поверхность, ограниченная контуром С. Единичный вектор нормали  выбирается так, что с его конца направление обхода С видно совершающимся против часовой стрелки. Тогда циркуляция поля
выбирается так, что с его конца направление обхода С видно совершающимся против часовой стрелки. Тогда циркуляция поля  по контуру С равна потоку ротора этого поля через поверхность
по контуру С равна потоку ротора этого поля через поверхность  :
:  .
.
Приведённую формулу называют формулой Стокса в векторной форме. В координатной форме формула Стокса имеет вид
 или
или
 .
.
Пример непосредственного вычисления циркуляции векторного поля и вычисления по формуле Стокса. Требуется вычислить циркуляцию поля  по контуру С, образующемуся в результате пересечения поверхности
по контуру С, образующемуся в результате пересечения поверхности  с координатными плоскостями.
с координатными плоскостями.

|
| x |
| y |
| z |
| O |
| A |
| B |
| D |
| C |

|

|
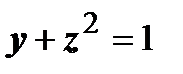
|
 :
: 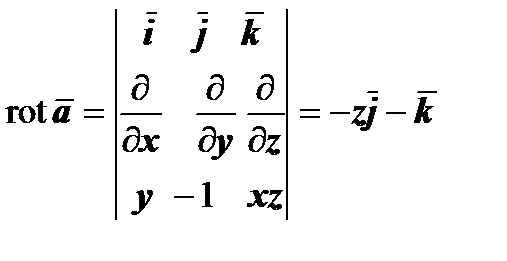 . Находим нормаль к
. Находим нормаль к  :
:  , знак взят с учётом того, что должно быть
, знак взят с учётом того, что должно быть  . Теперь
. Теперь  ; спроецируем
; спроецируем  на Охz:
на Охz:  ;
;  . Вычисляем
. Вычисляем 
 .
.
3)
1) Если ряд сходится, то сумма его остатка после n -го члена стремится к нулю при  .
.
Доказательство. Пусть S - сумма исходного ряда (18.2.1),  - сумма его остатка. Из равенства
- сумма его остатка. Из равенства  следует
следует  , т.е.
, т.е. 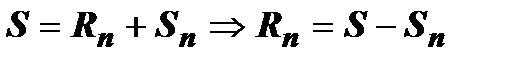 . Отсюда
. Отсюда  .
.
Здесь тоже можно сделать житейский вывод. Из предыдущего свойства следует, что сходимость ряда определяется сходимостью его остатка, т.е. хвостом ряда, а сумма S ряда, как следует из равенства  , о пределяется пределом
, о пределяется пределом  , т.е. началом ряда.
, т.е. началом ряда.
2) Если все члены сходящегося ряда умножить на одно и то же число с, то сходимость ряда сохранится, а сумма умножится на с.
Доказательство. Частичная сумма ряда  есть
есть  ; по свойству предела
; по свойству предела  .
.
3) Два сходящихся ряда  и
и 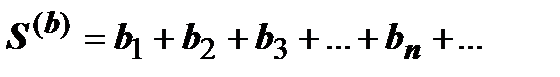 можно почленно складывать и вычитать; ряд
можно почленно складывать и вычитать; ряд  также сходится, и его сумма равна
также сходится, и его сумма равна  .
.
Доказательство и этого свойства - прямое следствие свойств пределов для частичных сумм:  .
.
4) 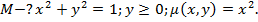
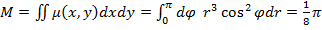
5) П-? 
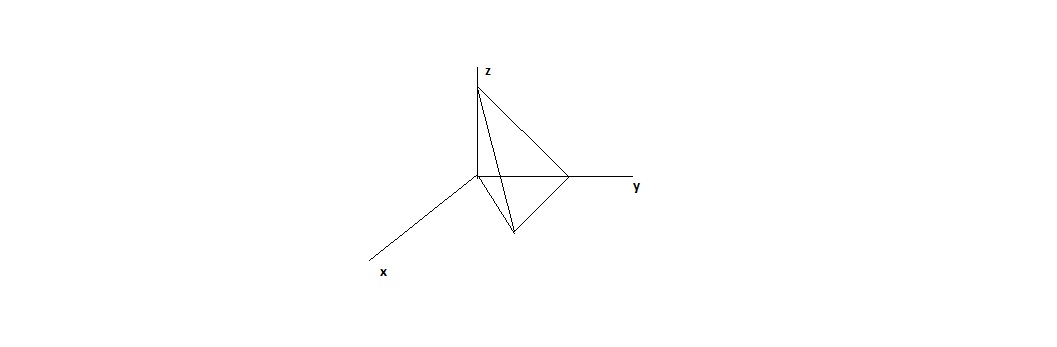
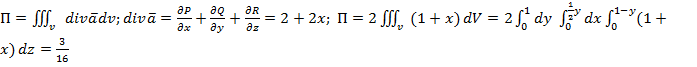
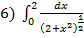
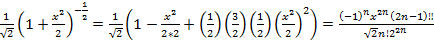
 (
(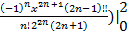
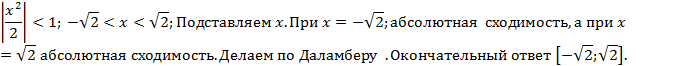
Билет 7.
1.
Определение потенциального поля. Векторное поле  (M) называется потенциальным в области V, если существует такое скалярное поле
(M) называется потенциальным в области V, если существует такое скалярное поле  , что
, что  (M)
(M) 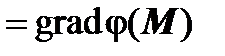 для
для  . Поле
. Поле  называется потенциалом поля
называется потенциалом поля  (M).
(M).

|

|
| х |
| у |

|
| O |
| G |

|
| z |
 и возьмём
и возьмём  , то
, то  , т.е. определённая таким образом функция
, т.е. определённая таким образом функция  действительно является потенциалом поля
действительно является потенциалом поля  (M). Это доказательство полностью повторяет доказательство теоремы пункта 16.3.3.6. Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути. Именно, требуется доказать, что
(M). Это доказательство полностью повторяет доказательство теоремы пункта 16.3.3.6. Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути. Именно, требуется доказать, что  . Действительно, пусть
. Действительно, пусть 
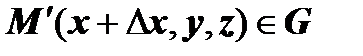 . Тогда
. Тогда  ,
,

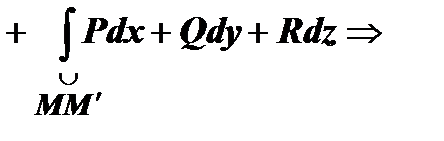
 (на
(на 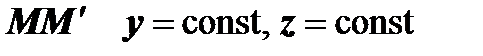 )
) 
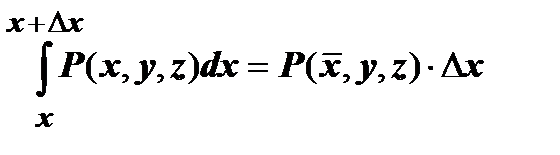 (по теореме о среднем)
(по теореме о среднем)  . Точка
. Точка  удовлетворяет условиям
удовлетворяет условиям  . Устремим
. Устремим  , тогда
, тогда  , и
, и  .
.
Аналогично доказывается, что  .
.
2.
Масса m материальной кривой  с плотностью m(x, y, z) вычисляется по формуле
с плотностью m(x, y, z) вычисляется по формуле  .
.
Пример. Найти массу четверти лемнискаты  , если плотность выражается формулой m(x, y)=
, если плотность выражается формулой m(x, y)=  .
.
Решение:  , поэтому
, поэтому 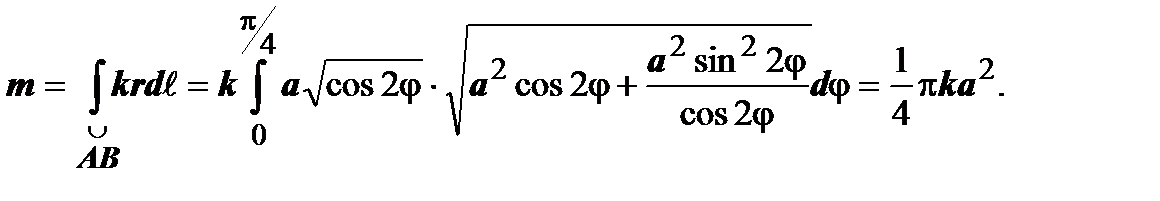
3.
Ряд  сходится равномерно на области G, если для любого числа
сходится равномерно на области G, если для любого числа  существует такое натуральное число
существует такое натуральное число  , одно и то же для всех точек
, одно и то же для всех точек  , что при n > N выполняется неравенство
, что при n > N выполняется неравенство  (или, что тоже самое,
(или, что тоже самое,  , где
, где  - остаток ряда после n -го члена).
- остаток ряда после n -го члена).
Признак Вейерштрасса. Если существует такой положительный сходящийся числовой ряд  , что члены функционального ряда
, что члены функционального ряда  в любой точке
в любой точке  удовлетворяют неравенству
удовлетворяют неравенству  , то функциональный ряд сходится равномерно в области G.
, то функциональный ряд сходится равномерно в области G.
Геометрическая прогрессия 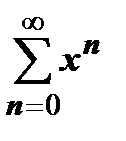 равномерно сходится на любом отрезке
равномерно сходится на любом отрезке  , целиком лежащем в области сходимости (-1, 1). Действительно, построим мажоранту для геометрической прогрессии на
, целиком лежащем в области сходимости (-1, 1). Действительно, построим мажоранту для геометрической прогрессии на  . Из чисел а, b выберем большее по модулю. Пусть, например,
. Из чисел а, b выберем большее по модулю. Пусть, например,  . Тогда для любого
. Тогда для любого  выполняется
выполняется  . Таким образом, сходящийся (так как
. Таким образом, сходящийся (так как  ) числовой ряд
) числовой ряд  мажорирует на
мажорирует на  функциональный ряд
функциональный ряд 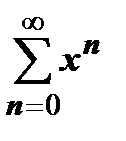 , откуда, по признаку Вейерштрасса, следует равномерная сходимость этого функционального ряда.
, откуда, по признаку Вейерштрасса, следует равномерная сходимость этого функционального ряда.
Ряд 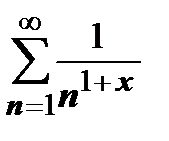 равномерно сходится на любой полуоси
равномерно сходится на любой полуоси  , так как на этом множестве он мажорируется рядом
, так как на этом множестве он мажорируется рядом  .
.
Ряд  равномерно сходится на всей числовой оси (мажоранта для этого ряда уже получена - это ряд
равномерно сходится на всей числовой оси (мажоранта для этого ряда уже получена - это ряд 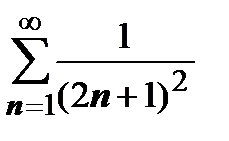 ).
).
4.
Окружность и гипербола.
Находим точки пересечения.
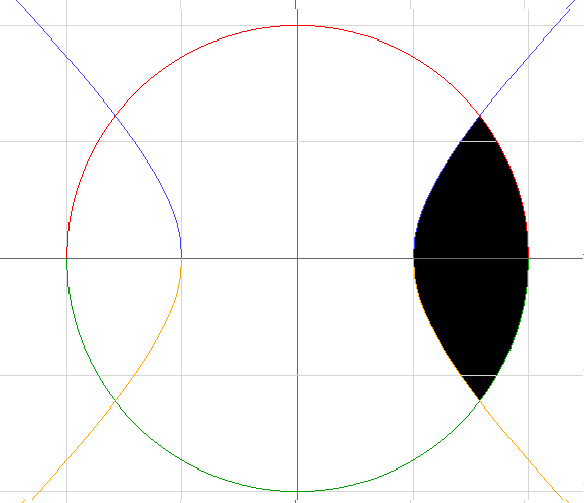 x=
x=  ; y1=
; y1= 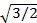 ; y2=
; y2= 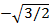
S = 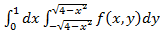 +
+  +
+  ;
;
S =  +
+ 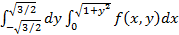 +
+  ;
;
В пол. коорд.
r< =2;
r< =1/ 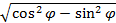
Точки пересечения
ϕ = ±arccos(1/4)
S = 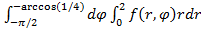 +
+  +
+ 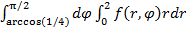
5.
Ввиду симметрии кривой, разобьем ее на 4 части
 ;
;  ;
;
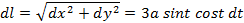
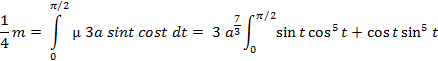
Замена p=sin t и q=cos t
Ответ m= 4 a^(7/3)
Билет 8.
1.
Определение криволинейного интеграла первого рода. Пусть в пространстве переменных x, y, z задана кусочно-гладкая кривая 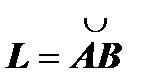 , на которой определена функция f (x, y, z).Разобьём кривую точками
, на которой определена функция f (x, y, z).Разобьём кривую точками  на
на 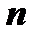 частей, на каждой из дуг
частей, на каждой из дуг  выберем произвольную точку
выберем произвольную точку  , найдём
, найдём  и длину
и длину  дуги
дуги  , и составим интегральную сумму
, и составим интегральную сумму  . Если существует предел последовательности интегральных сумм при
. Если существует предел последовательности интегральных сумм при  , не зависящий ни от способа разбиения кривой на дуги
, не зависящий ни от способа разбиения кривой на дуги  , ни от выбора точек
, ни от выбора точек  , то функция f (x, y, z) называется интегрируемой по кривой
, то функция f (x, y, z) называется интегрируемой по кривой  , а значение этого предела называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги от функции f (x, y, z) по кривой
, а значение этого предела называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги от функции f (x, y, z) по кривой  , и обозначается
, и обозначается  (или
(или  ).
).
Вычисление криволинейного интеграла первого рода. Примеры. Пусть кривая  задана параметрическими уравнениями
задана параметрическими уравнениями  , где
, где  - непрерывно дифференцируемые функции, и пусть точкам
- непрерывно дифференцируемые функции, и пусть точкам  , которые задают разбиение кривой, соответствуют значения параметра
, которые задают разбиение кривой, соответствуют значения параметра  , т.е.
, т.е.  . Тогда (см. раздел 13.3. Вычисление длин кривых)
. Тогда (см. раздел 13.3. Вычисление длин кривых)  . По теореме о среднем, существует точка
. По теореме о среднем, существует точка  такая, что
такая, что 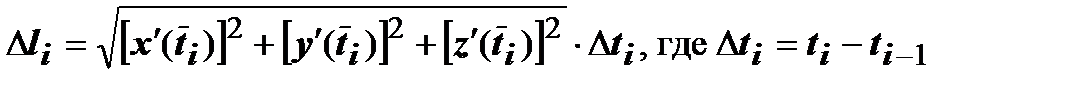 . Выберем точки
. Выберем точки  , получающиеся при этом значении параметра:
, получающиеся при этом значении параметра: 
 . Тогда интегральная сумма для криволинейного интеграла
. Тогда интегральная сумма для криволинейного интеграла  будет равна интегральной сумме для определенного интеграла
будет равна интегральной сумме для определенного интеграла  . Так как
. Так как  , то, переходя к пределу при
, то, переходя к пределу при  в равенстве
в равенстве  , получим
, получим
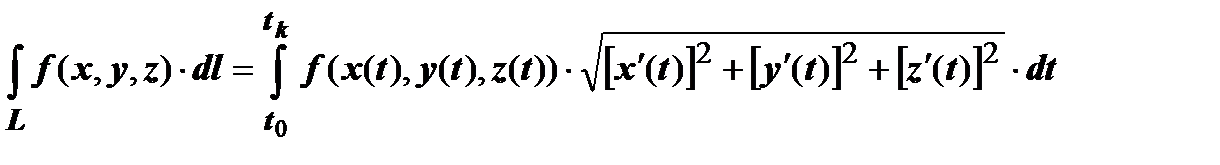 .
.
2.
Если существует предел последовательности интегральных сумм при  , не зависящий ни от способа разбиения кривой на дуги
, не зависящий ни от способа разбиения кривой на дуги  , ни от выбора точек
, ни от выбора точек  , то функция Р (x, y, z) называется интегрируемой по кривой
, то функция Р (x, y, z) называется интегрируемой по кривой  , а значение этого предела называется криволинейным интегралом второго рода, или криволинейным интегралом по координате х от функции Р (x, y, z) по кривой
, а значение этого предела называется криволинейным интегралом второго рода, или криволинейным интегралом по координате х от функции Р (x, y, z) по кривой  , и обозначается
, и обозначается  (или
(или  ).
).
Свойства криволинейного интеграла второго рода. Для этого интеграла существенны следующие свойства:
16.3.3.2.1. Линейность. Если функции  интегрируемы по кривой
интегрируемы по кривой  (каждая по своей координате, то по этой кривой интегрируемы функции
(каждая по своей координате, то по этой кривой интегрируемы функции  , и
, и 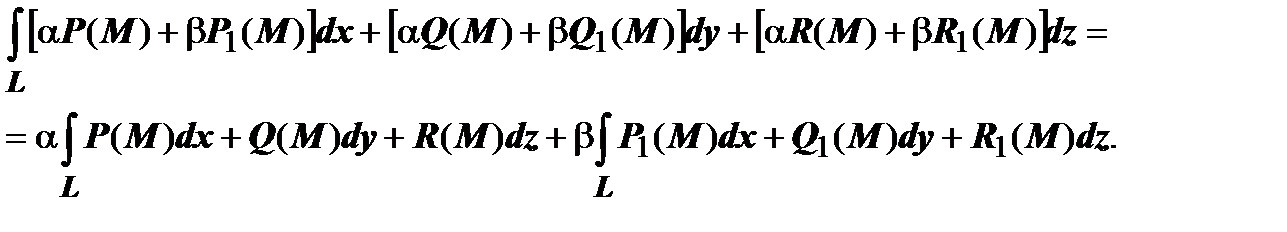
16.3.3.2.2. Аддитивность. Если кривая  разбита на две части
разбита на две части  и
и  , не имеющие общих внутренних точек, то
, не имеющие общих внутренних точек, то  .
.
16.3.3.2.3. Изменение знака криволинейного интеграла второго рода при изменении направления прохождения кривой:  .
.
4.
 rТочки пересечения (-4; 8) и (2; 2)
rТочки пересечения (-4; 8) и (2; 2)
S = 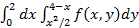
S = 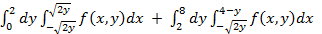
В полярных координатах
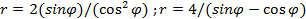
Точки пересечения 
S = 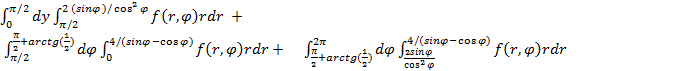
5.
 =
= 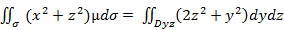
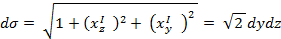
Переходим в обобщенные полярные координаты y=arcos  z=ar/
z=ar/ 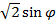
 rdr = ½ π a^4
rdr = ½ π a^4
6.
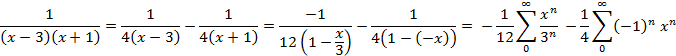
Сходится абсолютно при -1< x< 1
Билет 9.
1.
Определение криволинейного интеграла первого рода. Пусть в пространстве переменных x, y, z задана кусочно-гладкая кривая 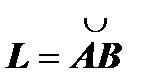 , на которой определена функция f (x, y, z).Разобьём кривую точками
, на которой определена функция f (x, y, z).Разобьём кривую точками  на
на 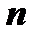 частей, на каждой из дуг
частей, на каждой из дуг  выберем произвольную точку
выберем произвольную точку  , найдём
, найдём  и длину
и длину  дуги
дуги  , и составим интегральную сумму
, и составим интегральную сумму  . Если существует предел последовательности интегральных сумм при
. Если существует предел последовательности интегральных сумм при  , не зависящий ни от способа разбиения кривой на дуги
, не зависящий ни от способа разбиения кривой на дуги  , ни от выбора точек
, ни от выбора точек  , то функция f (x, y, z) называется интегрируемой по кривой
, то функция f (x, y, z) называется интегрируемой по кривой  , а значение этого предела называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги от функции f (x, y, z) по кривой
, а значение этого предела называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги от функции f (x, y, z) по кривой  , и обозначается
, и обозначается  (или
(или  ).
).
Вычисление криволинейного интеграла первого рода. Примеры. Пусть кривая  задана параметрическими уравнениями
задана параметрическими уравнениями  , где
, где  - непрерывно дифференцируемые функции, и пусть точкам
- непрерывно дифференцируемые функции, и пусть точкам  , которые задают разбиение кривой, соответствуют значения параметра
, которые задают разбиение кривой, соответствуют значения параметра  , т.е.
, т.е.  . Тогда (см. раздел 13.3. Вычисление длин кривых)
. Тогда (см. раздел 13.3. Вычисление длин кривых)  . По теореме о среднем, существует точка
. По теореме о среднем, существует точка  такая, что
такая, что 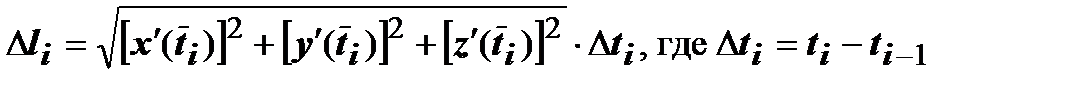 . Выберем точки
. Выберем точки  , получающиеся при этом значении параметра:
, получающиеся при этом значении параметра: 
 . Тогда интегральная сумма для криволинейного интеграла
. Тогда интегральная сумма для криволинейного интеграла  будет равна интегральной сумме для определенного интеграла
будет равна интегральной сумме для определенного интеграла  . Так как
. Так как  , то, переходя к пределу при
, то, переходя к пределу при  в равенстве
в равенстве  , получим
, получим
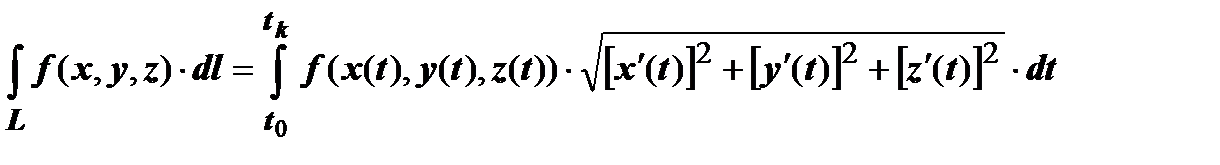 .
.
2.