Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дивергенцией(или расходимостью)векторного поля
|
|
в точке M называется скаляр вида 
и обозначается символом 
, т.е.
Свойства дивергенции:
1. Если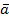 
– постоянный вектор, то 
2. 
3. 
4. Если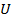 
- скалярная функция, 
–вектор, то 
Дивергенцией векторного поля в точке M называется предел отношения потока через замкнутую поверхность S, окружающую точку M, к объему тела, ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку M 
Дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном векторном.
Исходя из физического смысла потока(обычно условно считают, что 
есть поле скоростей фиктивного стационарного потока несжимаемой жидкости) можно сказать, что при 
точка M представляет собой источник, откуда жидкость вытекает; при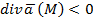 
точка M есть сток, поглощающий жидкость. Величина характеризует мощность источника или стока в точке M. В этом и состоит физический смысл дивергенции. При 
векторное поле называется соленоидальным, а это означает что в объеме нет ни стоков, ни источников(либо они компенсируются).
2. Криволинейный интеграл второго рода в декартовой системе координат. 
Пусть в плоскости 
задана непрерывная кривая 
и функция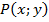 
, определенная в каждой точке кривой. Разобьем кривую 
точками 
в направлении от точки 
к точке 
на 
дуг 
с длинами 
На каждой «элементарной дуге»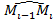 
возьмем точку 
и составим сумму вида 
, где 
= 
– проекция дуги на ось 
.
Такую сумму называют интегральной суммой для функции 
по переменной 
Если при 
интегральная сумма имеет конечный предел, не зависящий ни от способа разбиения кривой 
, ни от выбора точек , то его называют криволинейным интегралом по координате 
(или второго рода) от функции 
по кривой 
и обозначают:
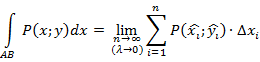
Аналогично вводится криволинейный интеграл от функции 
по координате 
:
Криволинейный интеграл второго рода общего вида определяется равенством
3. Вычислить массу поверхности полусферы 
, вырезанной цилиндром 
, если плотность оболочки полусферы 
.
4. Вычислить объем тела, огранич. пов. 
5. Разложить в ряд Маклорена функцию 
Билет №14
1. Свойства соленоидального поля
Векторное поле называется соленоидальным, если во всех точках его дивергенция поля равна нулю, т.е. 
Примерами соленоидальных полей являются: поле линейных скоростей вращающегося твердого тела; магнитное поле, создаваемое прямолинейным проводником, вдоль которого течет электрический ток.
Свойства: