Билет 12.

1 Вопрос) Циркуляция векторного поля. Циркуляцией называется линейный интеграл векторного поля по замкнутой кривой С: .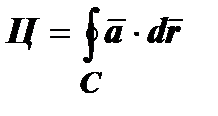

Обычно говорят, что циркуляция характеризует вращательную способность поля. Имеется в виду следующее. Если векторные линии поля замкнуты, то, как мы видели, циркуляция по ним в направлении поля положительна, при этом в гидродинамической интерпретации частицы жидкости крутятся по этим замкнутым линиям.

Ротор векторного поля. Ротором векторного поля (M) в точке называется векторная величина (векторное поле) = .

.

Смысл Ротора – характеризует закручивающую способность поля.

2 Вопрос) Определение единичного вектора нормали к поверхности. Выражения для элемента площади поверхности. Предположим, что поверхность задаётся неявным уравнением ( 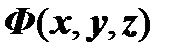- непрерывно дифференцируемая функция) и взаимно однозначно проецируется в область на плоскости Оху. , где знак перед дробью соответствует возможности выбора двух возможных взаимно противоположных направлений нормали. В координатной форме , то , , . Теперь мы можем выразить элемент площади поверхности через элемент площади в каждой координатной плоскости: , , .

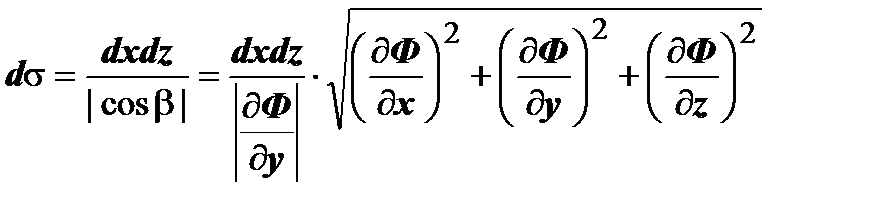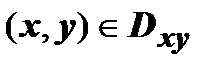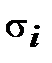Выражение поверхностного интеграла через двойной интеграл по проекции поверхности на координатную плоскость. Пустьповерхность взаимно однозначно проецируется в область на плоскости Оху. Будем считать, что поверхность задана уравнением , . В интегральной сумме выразим площадь через двойной интеграл по её проекции на плоскость Оху: . Применим к этому интегралу теорему о среднем: существует точка 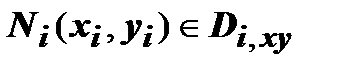такая, что 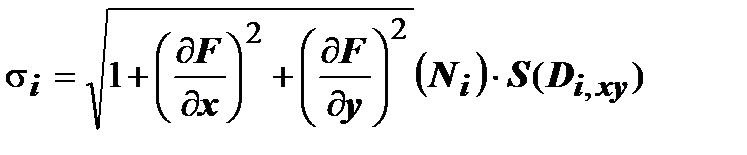. Значение подынтегральной функции 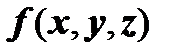будем вычислять в точке 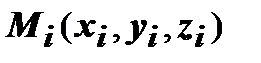, такой, что . Тогда .

.
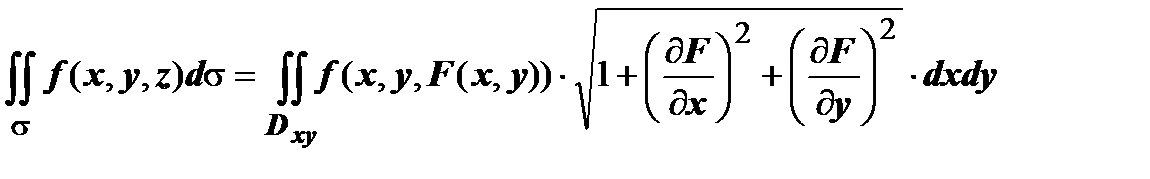