Главная страница
Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
|
Билет 10.
1.Теорема Грина для односвязной области. Пусть на плоскости Oxy задана односвязная область D, ограниченная кусочно-гладким контуром C. На множестве  определены непрерывные функции определены непрерывные функции  и и  , имеющие непрерывные частные производные. Тогда , имеющие непрерывные частные производные. Тогда  , при этом контур С обходится так, что область D остаётся слева. , при этом контур С обходится так, что область D остаётся слева.
Док-во. 1. Пусть D - простая область. Докажем сначала, что  . . Опишем D неравенствами  Тогда Тогда  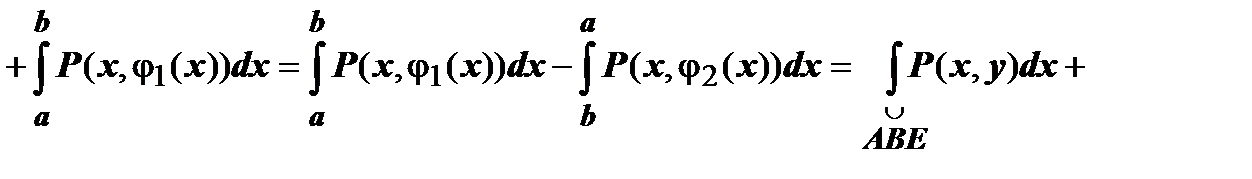 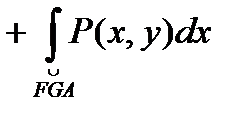 . Если контур включает вертикальные участки, такие как EF, то на этих участках dx = 0, поэтому . Если контур включает вертикальные участки, такие как EF, то на этих участках dx = 0, поэтому 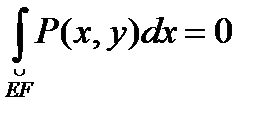 , и , и  , что и требовалось доказать. , что и требовалось доказать.
Равенство 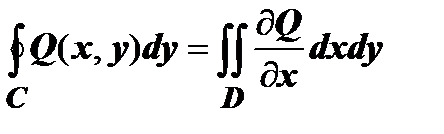 доказывается точно также: доказывается точно также:    . Суммируя равенства . Суммируя равенства  и и 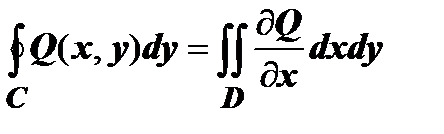 , получим одну из важнейших формул анализа -формулу Грина , получим одну из важнейших формул анализа -формулу Грина

2. Пусть теперь D - произвольная, не обязательно простая, область. Разобьём её на простые части. Пусть это разбиение производится отрезком АВ, и пусть подобласти D 1 и D 2 - результат разбиения. Для этих подобластей формула Грина доказана:
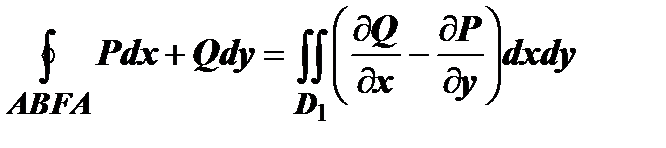 и и 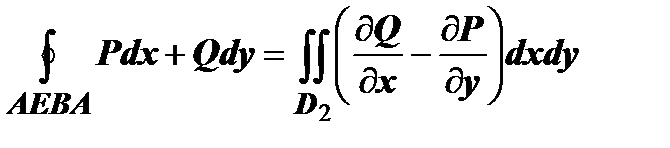 . По свойству аддитивности . По свойству аддитивности 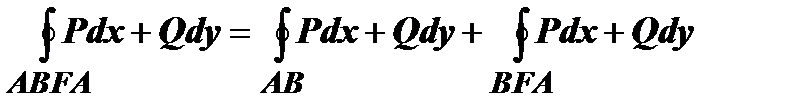 , , 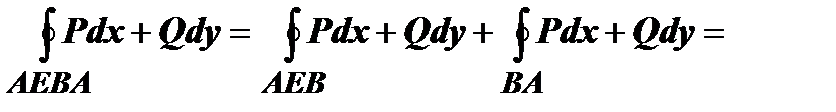 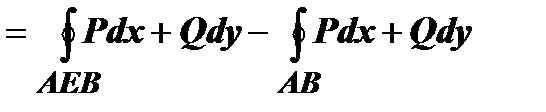 . Суммируя эти выражения, убеждаемся, что криволинейные интегралы по отрезкам АВ и ВА взаимно уничтожаются, а сумма интегралов по кривым ВFA и AEB даёт интеграл по контуру С, т.е. формула Грина верна и для области, не являющейся простой. Доказательство остаётся справедливым и в случае, когда разбиение производится добавлением большего числа, чем одна, кривых. . Суммируя эти выражения, убеждаемся, что криволинейные интегралы по отрезкам АВ и ВА взаимно уничтожаются, а сумма интегралов по кривым ВFA и AEB даёт интеграл по контуру С, т.е. формула Грина верна и для области, не являющейся простой. Доказательство остаётся справедливым и в случае, когда разбиение производится добавлением большего числа, чем одна, кривых.
2. Выпишите формулу для вычисления поверхностного интеграла 1 рода в декартовой системе координат. приведите пример.
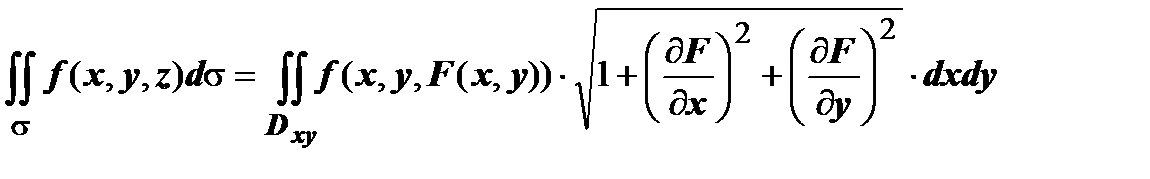
Пример: вычилить поверхностный интеграл
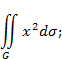
G: x+y+z=1, первый октант
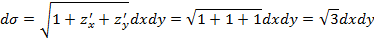
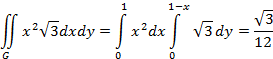
3. Теорема. Для того, чтобы бесконечно дифференцируемая функция 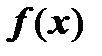 в окрестности точки в окрестности точки  разлагалась в ряд Тейлора, необходимо и достаточно, чтобы разлагалась в ряд Тейлора, необходимо и достаточно, чтобы  . .
Доказательство. Необходимость. Пусть в окрестности точки  функция функция 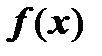 представлена в виде сходящегося к этой функции ряда Тейлора представлена в виде сходящегося к этой функции ряда Тейлора  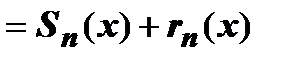 , где , где  - частичная сумма ряда, - частичная сумма ряда,  - его остаток. Так как - его остаток. Так как 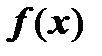 имеет требуемое количество производных, она может быть представлена и в виде формулы Тейлора с остаточным членом в форме Лагранжа: имеет требуемое количество производных, она может быть представлена и в виде формулы Тейлора с остаточным членом в форме Лагранжа:  . Сравнивая эти представления, получаем . Сравнивая эти представления, получаем 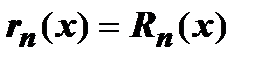 . Из сходимости ряда к . Из сходимости ряда к 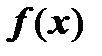 следует, что следует, что  , что и требовалось доказать. , что и требовалось доказать.
Достаточность. Если  , то , то  , т.е. остаток ряда стремится к нулю при , т.е. остаток ряда стремится к нулю при  , т.е. ряд сходится к функции , т.е. ряд сходится к функции 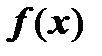 . .
4. Найдите поток векторного поля a=xi+4yj+(5z+1)k через плоскость x+2y+z/2=1, расположенную в первом октанте, нормаль образует острый угол с осью oz.
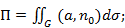 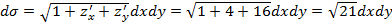 , , 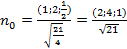 ; ; 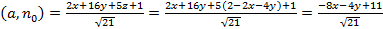
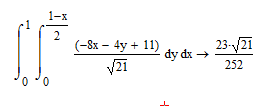
5. Найдите циркуляцию поля 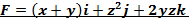 вдоль контура Г, ориентированного по вектору k, если Г- пересечение поверхностей вдоль контура Г, ориентированного по вектору k, если Г- пересечение поверхностей 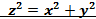 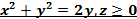
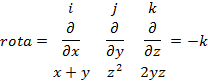
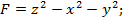
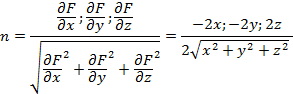
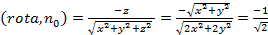 ; ;

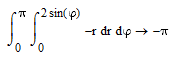
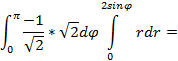
|

 определены непрерывные функции
определены непрерывные функции  и
и  , имеющие непрерывные частные производные. Тогда
, имеющие непрерывные частные производные. Тогда  , при этом контур С обходится так, что область D остаётся слева.
, при этом контур С обходится так, что область D остаётся слева. .
. 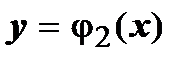
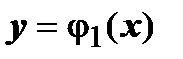
 Тогда
Тогда 
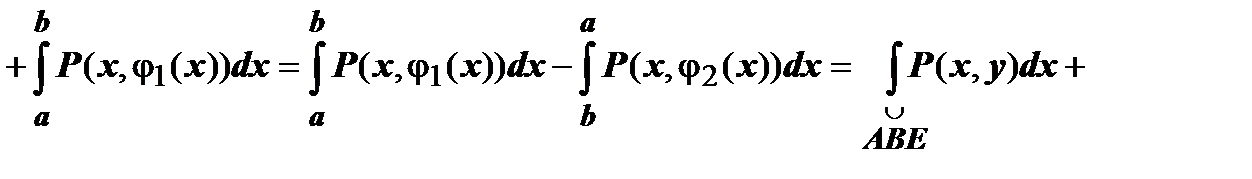
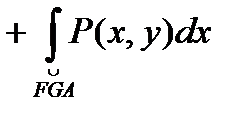 . Если контур включает вертикальные участки, такие как EF, то на этих участках dx = 0, поэтому
. Если контур включает вертикальные участки, такие как EF, то на этих участках dx = 0, поэтому 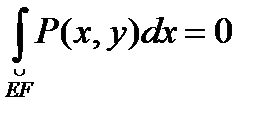 , и
, и 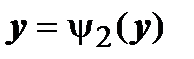
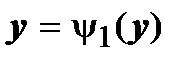
 , что и требовалось доказать.
, что и требовалось доказать.
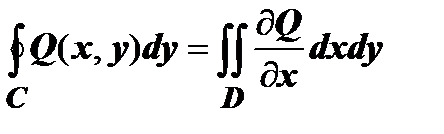 доказывается точно также:
доказывается точно также: 

 . Суммируя равенства
. Суммируя равенства  и
и 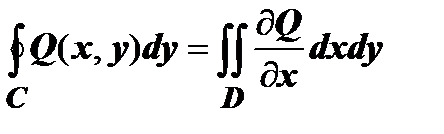 , получим одну из важнейших формул анализа -формулу Грина
, получим одну из важнейших формул анализа -формулу Грина
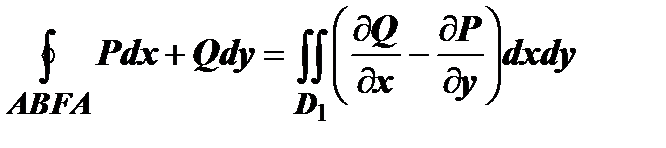 и
и 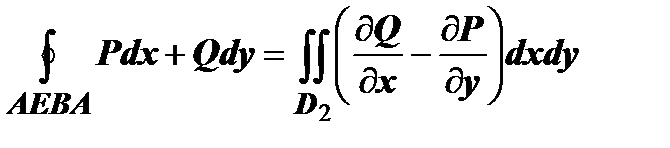 . По свойству аддитивности
. По свойству аддитивности 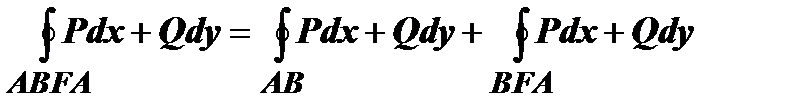 ,
, 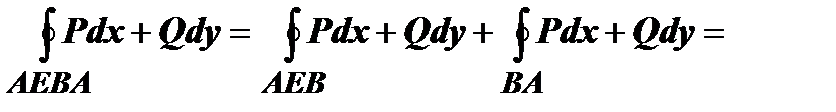
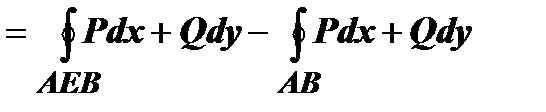 . Суммируя эти выражения, убеждаемся, что криволинейные интегралы по отрезкам АВ и ВА взаимно уничтожаются, а сумма интегралов по кривым ВFA и AEB даёт интеграл по контуру С, т.е. формула Грина верна и для области, не являющейся простой. Доказательство остаётся справедливым и в случае, когда разбиение производится добавлением большего числа, чем одна, кривых.
. Суммируя эти выражения, убеждаемся, что криволинейные интегралы по отрезкам АВ и ВА взаимно уничтожаются, а сумма интегралов по кривым ВFA и AEB даёт интеграл по контуру С, т.е. формула Грина верна и для области, не являющейся простой. Доказательство остаётся справедливым и в случае, когда разбиение производится добавлением большего числа, чем одна, кривых.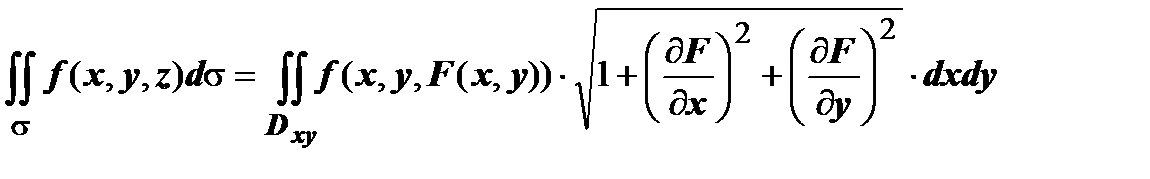
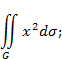
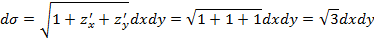
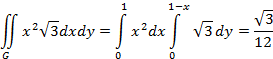
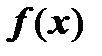 в окрестности точки
в окрестности точки  разлагалась в ряд Тейлора, необходимо и достаточно, чтобы
разлагалась в ряд Тейлора, необходимо и достаточно, чтобы  .
. функция
функция 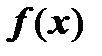 представлена в виде сходящегося к этой функции ряда Тейлора
представлена в виде сходящегося к этой функции ряда Тейлора 
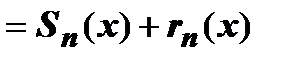 , где
, где  - частичная сумма ряда,
- частичная сумма ряда,  - его остаток. Так как
- его остаток. Так как 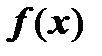 имеет требуемое количество производных, она может быть представлена и в виде формулы Тейлора с остаточным членом в форме Лагранжа:
имеет требуемое количество производных, она может быть представлена и в виде формулы Тейлора с остаточным членом в форме Лагранжа:  . Сравнивая эти представления, получаем
. Сравнивая эти представления, получаем 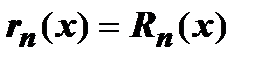 . Из сходимости ряда к
. Из сходимости ряда к 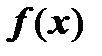 следует, что
следует, что  , что и требовалось доказать.
, что и требовалось доказать. , то
, то  , т.е. остаток ряда стремится к нулю при
, т.е. остаток ряда стремится к нулю при  , т.е. ряд сходится к функции
, т.е. ряд сходится к функции 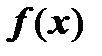 .
.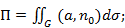
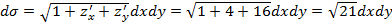 ,
, 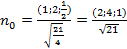 ;
; 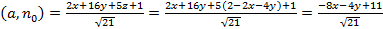
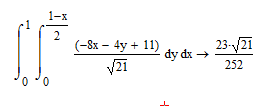
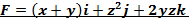 вдоль контура Г, ориентированного по вектору k, если Г- пересечение поверхностей
вдоль контура Г, ориентированного по вектору k, если Г- пересечение поверхностей 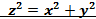
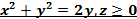

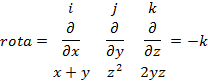
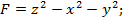
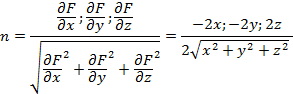
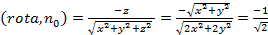 ;
;