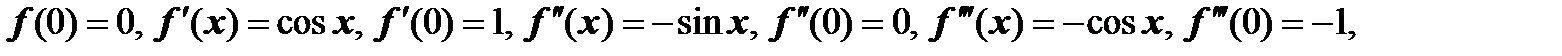Сформулируйте и докажите свойства соленоидального векторного поля. (6 баллов)

Определение соленоидального поля. Векторное поле а (M) называется соленоидаль-ным в области V, если во всех точках этой области div= M(a)=0.

Согласно этому определению, поле не может иметь в области V источников и стоков; таким свойством обладает магнитное поле соленоида, что и объясняет происхождение термина.

Соленоидально поле ротора любого достаточно гладкого поля: rotdivM(a)=0.

18.2.2. Свойства соленоидального поля.

1. Поток соленоидального векторного поля через поверхность σ, ограничивающую область V ∈ σ, равен нулю. Это прямое следствие формулы Остроградского.

2. Верно и обратное утверждение: равенство нулю потока через любую замкнутую поверхность σ достаточно для соленоидальности поля (M).

3. Пусть в V имеется изолированный источник (или сток) поля. Если поле (M) соле-ноидально, то его поток через любую замкнутую поверхность σ, содержащую этот источник, имеет одно и то же значение.

Фраза " в V имеется изолированный источник (или сток) поля" означает, что об-ласть V, в которой поле соленоидально, неодносвязна; из V выколота точка, в которой находится источник.

Поток соленоидального векторного поля через любое поперечное сечение вектор-ной трубки один и тот же. Это следует из того, что поток через боковую поверх-ность трубки равен нулю.

Напишите разложение в ряд Маклорена основных элементарных функций и укажите области пригодности таких разложений. (6 баллов)

.

Все производные этой функции в точке х=0 равны 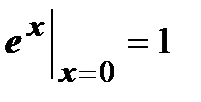, поэтому ряд имеет вид

.

Область сходимости этого ряда - вся числовая ось (пример 6 раздела 18.2.4.3. Радиус сходимости, интервал сходимости и область сходимости степенного ряда), поэтому при. Как следствие, остаточный член формулы Тейлора. Поэтому ряд сходится к в любой точке х.

3..

Здесь