
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Почленно интегрируя ряд , получим разложение для функции . Выполнить все выкладки самостоятельно, выписать область сходимости.
|
|
9. Выпишем разложение функции 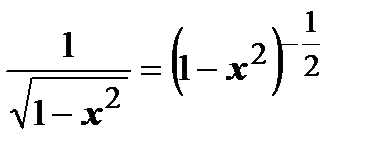 по формуле биномиального ряда с
по формуле биномиального ряда с  :
: 
 . Знаменатель
. Знаменатель  представлен как
представлен как  , двойной факториал
, двойной факториал  означает произведение всех натуральных чисел той же чётности, что и
означает произведение всех натуральных чисел той же чётности, что и  , не превосходящих
, не превосходящих  . Разложение сходится к функции при
. Разложение сходится к функции при  . Почленно интегрируя его от 0 до х, получим
. Почленно интегрируя его от 0 до х, получим  . Оказывается, что этот ряд сходится к функции на всём отрезке
. Оказывается, что этот ряд сходится к функции на всём отрезке  ; при х=1 получаем ещё одно красивое представление числа
; при х=1 получаем ещё одно красивое представление числа  :
:  .
.
4. Расставьте пределы интегрирования в двойном интеграле, поменяйте порядок интегрирования, перейдите к полярным координатам, если y  x+y
x+y 
 .(4 балла).
.(4 балла).
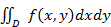 =
=  +
+  =
=  +
+  =
=  +
+  -
-  .
.
6. Исследуйте на сходимость.

 )
) 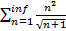 -расходится, т.к. не соблюдается необходимый признак сходимости.
-расходится, т.к. не соблюдается необходимый признак сходимости.
Sin(б.б.в) расходится, т.к. не соблюдается признак Лейбница.
Значит данный ряд расходится.

Применим признак Даламбера.
Ряд из модулей расходится, т.е. ряд расходится абсолютно. Не выполняется признак Лейбница, ряд расходится.
Ответ: два заданных ряда расходящиеся.РяРя
Билет 18.
1).Несобственным двойным интегралом первого рода называется несобственный интеграл по неограниченной поверхности. Построим области G, такие, что каждая последующая область вклюяает в себя предыдущую, и области уходят в бесконечность. Рассматривая интеграл по областям яв-ся пересечением области D и G. Если все эти интегралы имеют конечный предел, то он сходится, в другом случае расходится.
П= 
 .
.
Построим области, которые яв-ся окружностями с центром в начале координат, чьи радиусы уходят в бесконечность. Перейдем в полярные координаты и возьмем данный интеграл.
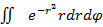 =(при r-> inf)=
=(при r-> inf)=  .
.
 =
=  =π.
=π.
Заключаем, что П=  .
.
2).. Ротор векторного поля. Ротором векторного поля  (M) в точке
(M) в точке  называется векторная величина (векторное поле)
называется векторная величина (векторное поле)  . Запомнить эту формулу очень легко, если выразить
. Запомнить эту формулу очень легко, если выразить  через оператор Гамильтона набла:
через оператор Гамильтона набла:  равен векторному произведению
равен векторному произведению  . Действительно,
. Действительно,  . Если теперь раскрыть этот определитель по первой строке, получим
. Если теперь раскрыть этот определитель по первой строке, получим
 .
.
Пример: если  , то
, то 
 Свойства ротора:
Свойства ротора:
1. Если  (M) - постоянное векторное поле, то
(M) - постоянное векторное поле, то  ;
;
2.  (или
(или  );
);
3. Если u - скалярное поле, то  (или
(или 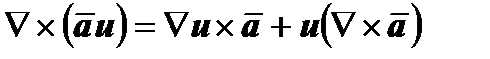 ). В частности, если
). В частности, если  (M) - постоянное векторное поле, то
(M) - постоянное векторное поле, то  .
.
Докажем третье свойство. 


.
Инвариантное определение ротора. Пусть  . Возьмём малую плоскую площадку
. Возьмём малую плоскую площадку  , ограниченную контуром С. По теореме Стокса циркуляция по С равна
, ограниченную контуром С. По теореме Стокса циркуляция по С равна  . Считая, что
. Считая, что  мало меняется на
мало меняется на  , и что поверхностный интеграл равен
, и что поверхностный интеграл равен  , получим
, получим 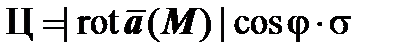 . Будем теперь крутить площадку вокруг точки М, при этом циркуляция меняется вместе с
. Будем теперь крутить площадку вокруг точки М, при этом циркуляция меняется вместе с  . Максимальное значение циркуляция получит при
. Максимальное значение циркуляция получит при  , т.е. когда направления
, т.е. когда направления  и
и  совпадут. Следовательно,
совпадут. Следовательно,  указывает направление, вокруг которого циркуляция максимальна и равна
указывает направление, вокруг которого циркуляция максимальна и равна  . Модуль ротора определяется соотношением
. Модуль ротора определяется соотношением  .
.
2).. Если степенной ряд сходится в точке 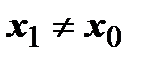 , то
, то
1. он абсолютно сходится в любой точке х, удовлетворяющей неравенству  (т.е. находящейся ближе к точке
(т.е. находящейся ближе к точке 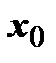 , чем
, чем  );
);
2. он сходится равномерно на любом отрезке  , целиком лежащем на интервале
, целиком лежащем на интервале  (т.е. на интервале с центром в
(т.е. на интервале с центром в 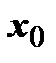 радиуса
радиуса  ).
).
3. Если этот ряд расходится в точке  , то он расходится в любой точке х, удовлетворяющей неравенству
, то он расходится в любой точке х, удовлетворяющей неравенству  (т.е. находящейся дальше от точки
(т.е. находящейся дальше от точки 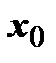 , чем
, чем  ).
).
| ) |
| ( |
| х |
| ) |
| ( |
| х 0 |
| х 1 |
| х 2 |
| сходимость |
| расходимость |
| расходимость |
| а |
| b |
 в точке
в точке  следует, что его общий член
следует, что его общий член  стремится к нулю при
стремится к нулю при  ; любая последовательность, имеющая предел, ограничена, следовательно, существует число С такое, что
; любая последовательность, имеющая предел, ограничена, следовательно, существует число С такое, что  . Пусть точка х удовлетворяет неравенству
. Пусть точка х удовлетворяет неравенству  , тогда
, тогда  . Оценим член ряда в точке х:
. Оценим член ряда в точке х:
 . Члены ряда в точке х по абсолютной величине не превосходят членов сходящейся геометрической прогрессии, следовательно, ряд сходится абсолютно в точке х, следовательно, он сходится абсолютно в любой точке интервала
. Члены ряда в точке х по абсолютной величине не превосходят членов сходящейся геометрической прогрессии, следовательно, ряд сходится абсолютно в точке х, следовательно, он сходится абсолютно в любой точке интервала  .
.
2. Пусть отрезок  , целиком лежит на интервале
, целиком лежит на интервале  . Из точек а, b выберем ту, которая находится дальше от точки
. Из точек а, b выберем ту, которая находится дальше от точки 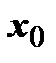 , примем для определённости, что это - точка а:
, примем для определённости, что это - точка а:  . Тогда для любого х из этого отрезка
. Тогда для любого х из этого отрезка 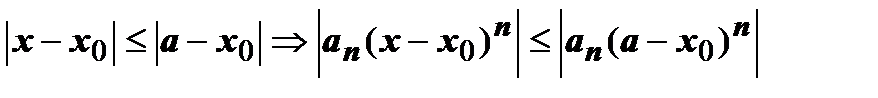 . В точке
. В точке  ряд
ряд  , по доказанному, сходится абсолютно, но он является на
, по доказанному, сходится абсолютно, но он является на  мажорантой для ряда
мажорантой для ряда  , следовательно, степенной ряд сходится равномерно на отрезке
, следовательно, степенной ряд сходится равномерно на отрезке  .
.
3. Пусть степенной ряд расходится в точке  , и
, и  . То, что ряд расходится в точке х, докажем от противного. Если предположить, что он сходится в точке х, то, по доказанному, он сходится во всех точках, расположенных ближе к
. То, что ряд расходится в точке х, докажем от противного. Если предположить, что он сходится в точке х, то, по доказанному, он сходится во всех точках, расположенных ближе к 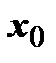 , чем х, следовательно, он сходится в точке
, чем х, следовательно, он сходится в точке  , что противоречит условию.
, что противоречит условию.
. Радиус сходимости, интервал сходимости и область сходимости степенного ряда. Из теоремы Абеля следует, что существует такое число R  (возможно,
(возможно,  ) такое, что при
) такое, что при  степенной ряд сходится, при
степенной ряд сходится, при  ряд расходится. Действительно, пусть в точке
ряд расходится. Действительно, пусть в точке  ряд сходится, в точке
ряд сходится, в точке  ряд расходится. Рассмотрим точку
ряд расходится. Рассмотрим точку  , расположенную между областями, в которых установлена сходимость и расходимость. В точке
, расположенную между областями, в которых установлена сходимость и расходимость. В точке  числовой ряд
числовой ряд 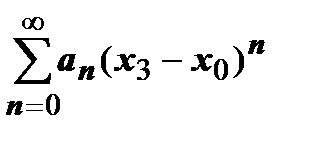 либо сходится, либо расходится. Если он сходится, то мы можем перенести точку
либо сходится, либо расходится. Если он сходится, то мы можем перенести точку  в точку
в точку  ; если ряд в точке
; если ряд в точке  расходится, мы переносим в
расходится, мы переносим в  точку
точку  . Продолжая этот процесс, мы сблизим точки
. Продолжая этот процесс, мы сблизим точки  и
и  , эта граница и определит число R.
, эта граница и определит число R.
Определение. Число R  такое, что при
такое, что при  степенной ряд сходится, при
степенной ряд сходится, при  ряд расходится, называется радиусом сходимости. Интервал
ряд расходится, называется радиусом сходимости. Интервал  называется интервалом сходимости степенного ряда.
называется интервалом сходимости степенного ряда.
Сходимость ряда в концевых точках интервала сходимости должна исследоваться отдельно. В зависимости от поведения ряда на концах интервала сходимости область сходимости степенного ряда может быть одной из следующих:  ,
,  ,
,  ,
,  .
.
Итак, для определения области сходимости степенного ряда надо найти его интервал сходимости R, затем исследовать поведения ряда в концевых точках интервала сходимости  .
.
Примеры. 1.  . Для определения радиуса сходимости этого ряда целесообразно применить признак сходимости Дирихле. Однако этот признак, как и многие другие, может применяться только к положительному ряду, поэтому выпишем ряд, состоящий из абсолютных величин членов исследуемого ряда:
. Для определения радиуса сходимости этого ряда целесообразно применить признак сходимости Дирихле. Однако этот признак, как и многие другие, может применяться только к положительному ряду, поэтому выпишем ряд, состоящий из абсолютных величин членов исследуемого ряда:  . Применяем признак Дирихле:
. Применяем признак Дирихле:  . Следовательно,
. Следовательно,  . Мы нашли радиус сходимости R =3 и интервал сходимости
. Мы нашли радиус сходимости R =3 и интервал сходимости  . Исследуем поведение ряда на концах интервала:
. Исследуем поведение ряда на концах интервала:  , ряд сходится.
, ряд сходится.  , ряд сходится абсолютно. Область сходимости - интервал [-7, 7].
, ряд сходится абсолютно. Область сходимости - интервал [-7, 7].
4). 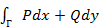 =
=  )dxdy – формула Грина
)dxdy – формула Грина
P=x+2y Q= 
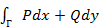 =
=  )dxdy=2
)dxdy=2  -2
-2  =
=  .
.
5).z=  -элиптический параболоид
-элиптический параболоид
Z=4-  => z=-(
=> z=-(  - эллиптический параболоид
- эллиптический параболоид
Перейдем в цилиндрические координаты
V=  =4π.
=4π.