Свойства потенциального поля. 1. Потенциал определён с точностью до произвольной постоянной ( ).

1. Потенциал определён с точностью до произвольной постоянной ().

2. Разность потенциалов в двух точках определена однозначно.

3. Если поле (M) потенциально, то линейный интеграл этого поля по любой кривой , целиком лежащей в V, определяется только начальной и конечной точками этой кривой, и не зависит от формы кривой. . Эта формула, как и в плоском случае, является обобщением формулы Ньютона-Лейбница для потенциального поля.

4. Циркуляция потенциального в области V поля по любому контуру, лежащему в V, равна нулю.

5. Векторная линия потенциального поля в каждой точке М ортогональна эквипотенциальной поверхности (т.е. поверхности уровня потенциала), проходящей через точку М.

6. Ротор потенциального векторного поля равен нулю:

.

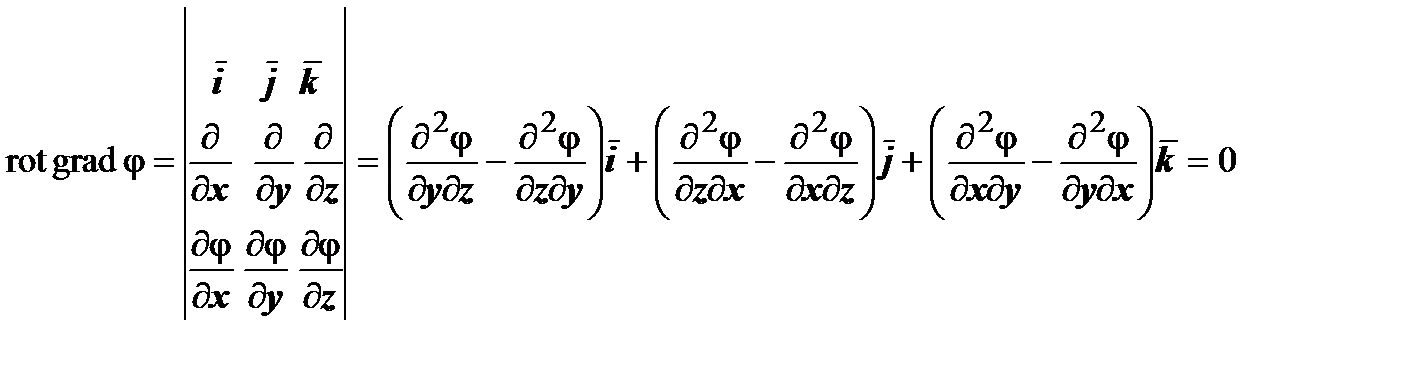Введём определение безвихревого поля: поле (M), ротор которого в каждой точке равен нулю, называется безвихревым.

Мы доказали, что потенциальное поле необходимо безвихрево. Дальше мы займёмся достаточными условиями потенциальности.