Задача 4. Изобразить поверхность исследовав ее методом параллельного сечения.

Изобразить поверхность исследовав ее методом параллельного сечения.

Решение.

Приведем данное уравнение к каноническому виду: т.е разделим правую и левую части исходного уравнения на 64 и получи: .

1) Рассмотрим сечение данной поверхности плоскостями , параллельными плоскости .

Раскроем модуль: . Тогда уравнение запишется в виде:

.

ОДЗ: .

.

Разделим правую и левую части уравнения на , получим: .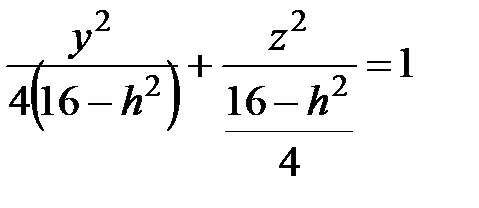

В сечении эллипсоида данными плоскостями, мы будем получать эллипсы разных полуосей.

Причем, при мы получим эллипс, который имеет максимальное значение полуосей: .

При и значение полуосей будет уменьшаться.

При получаем систему уравнений

Данной системе уравнений удовлетворяют точки с координатами 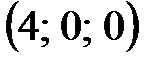и . В данных точках и эллипсоид пересекает ось

2) Рассмотрим сечение поверхности плоскостями , параллельными плоскости .

Раскроем модуль: . Следовательно, исходное уравнение примет вид: .

Аналогично первому случаю находим ОДЗ. ОДЗ: .

Разделим обе части уравнения на , получаем: .

В сечении эллипсоида данными плоскостями, мы будем получать эллипсы разных полуосей. Причем, при мы получим эллипс, который имеет максимальное значение полуосей: .

При и значение полуосей будет уменьшаться.

При , (решая аналогично 1), получаем две точки с координатами и . В данных точках и эллипсоид пересекает ось .

3) Рассмотрим сечение поверхности плоскостями , параллельными плоскости .

Раскроем модуль: . Значит исходное уравнение примет вид: .

ОДЗ: . После деления данного уравнения на правую часть получим уравнение: , при

В сечении эллипсоида данными плоскостями, мы будем получать эллипсы разных полуосей. Причем, при 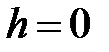мы получим эллипс, который имеет максимальное значение полуосей: .

При и значение полуосей будет уменьшаться.

При мы получим две точки с координатами и .

В данных точках и эллипсоид пересекает ось .

Рисунок 108