
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Домашнее задание № 6
|
|
1 Привести поверхности к каноническому виду и изобразить.
1) 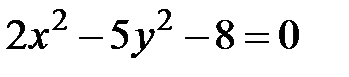 ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6) 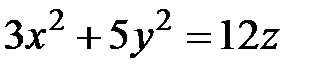 ;
;
7)  ; 8)
; 8) 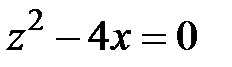 ;
;
9) 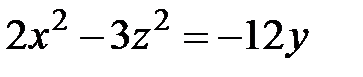 ; 10)
; 10) 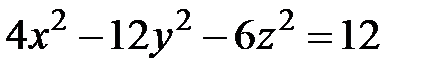 .
.
Ответ.
1) Гиперболический цилиндр с образующими, параллельными оси 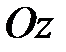 .
.
2) Конус.
3) Однополостной гиперболоид.
4) Параболический цилиндр с образующими, параллельными оси  .
.
5) Конус, у которого ось совпадает с осью 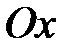 :
:  .
.
6) Эллиптический параболоид:  .
.
7) Эллиптический цилиндр с образующими, параллельными оси  .
.
8) Параболический цилиндр:  , с образующими, параллельными оси
, с образующими, параллельными оси 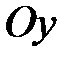 .
.
9) Гиперболический параболоид:  .
.
10) Двуполостной гиперболоид:  .
.
2 Какую поверхность определяет уравнение  ?
?
Ответ. В пространстве уравнение определяет прямой круговой цилиндр, для которого данная окружность служит направляющей. Образующие цилиндра параллельны оси  , причем сама ось является одной из образующих, так как данная окружность проходит через начало координат
, причем сама ось является одной из образующих, так как данная окружность проходит через начало координат
3 Какую поверхность определяет уравнение  ?
?
Ответ. Прямой круговой цилиндр, образующие которого параллельны оси 
4 Какая линия задана системой уравнений:
а) 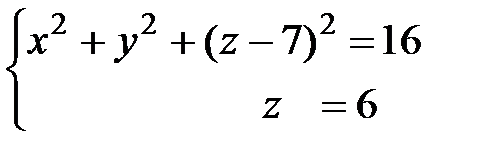 , б)
, б)  , в)
, в) 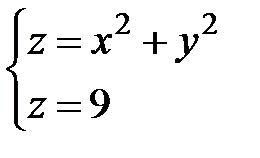 , г)
, г)  ?
?
(поверхности изобразить)
Ответ. а) Окружность:  , б) Эллипс:
, б) Эллипс: 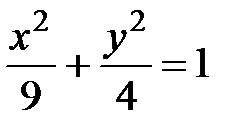 ,
,
в) Окружность: 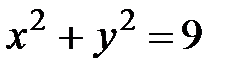 , г) Парабола:
, г) Парабола: 
5 Какие поверхности определяют уравнения
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ?
?
(поверхности изобразить)
Ответ.
1)  - уравнение гиперболического цилиндра;
- уравнение гиперболического цилиндра;
2)  - уравнение параболического цилиндра;
- уравнение параболического цилиндра;
3) 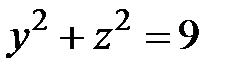 - уравнение прямого кругового цилиндра;
- уравнение прямого кругового цилиндра;
4)  - уравнение эллиптического цилиндра,
- уравнение эллиптического цилиндра,
Образующие всех этих цилиндрических поверхностей параллельны оси 