Задача 5. Вывести уравнение геометрического места точек, разность расстояний которых до двух данных точек и есть величина постоянная равная 6.

Вывести уравнение геометрического места точек, разность расстояний которых до двух данных точек и есть величина постоянная равная 6.

Решение.

Возьмем произвольную точку в пространстве . Тогда ; .

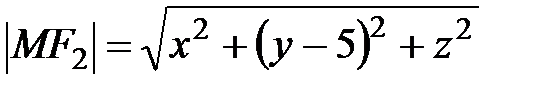Так как разность расстояний до двух данных точек и есть величина постоянная равная 6, то имеем следующее выражение

.

Раскроем модуль и возведем в квадрат левую и правую части равенства.

,

. Упростим данное равенство и корень квадратный перенесем в левую часть, а все остальное в правую часть.

.

.

Еще раз возведем в квадрат левую и правую части равенства.

.

Раскроем скобки, упростим выражение и приведем к каноническому виду. ,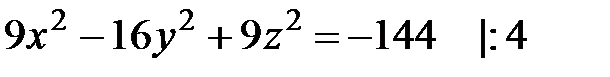

- двуполостный гиперболоид.

Ответ.

Задача 6

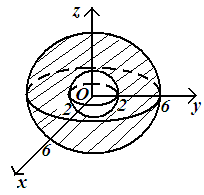
Изобразить тело, которое определяется следующим соотношением .

Решение.

Уравнения и определяют сферы с общим центром в точке с координатами и радиусами , соответственно. Рисунок 109

Множество точек пространства, которые равноудалены от точки на расстояние не менее 2 и не более 6.