Пример 3.9.

Пусть имеем степенную зависимость

,

где

- константа, значение которой известно.

Замена фактора:

.

ЗАДАЧА 2. Оценка «тесноты» связи между переменными.

1.Оценка «тесноты» и направления линейной связи.

Для оценки «тесноты» и направления линейной связи между двумя переменными используется коэффициент корреляции:

;

Для примера 3.6:

.

Диапазон изменения коэффициента корреляции: .

Считают:

- связь очень слабая;

- связь сильная;

- связь есть.

2.Оценка «тесноты» связи при любой форме связи.

Для оценки «тесноты» связи при любой форме связи и любом количестве факторов используется корреляционное отношение:

,

где

- коэффициент детерминации.

Диапазон изменения корреляционного отношения: .

Если разница между и не превышает , то принимают линейную форму связи между переменными.

Коэффициент детерминации показывает долю общей колеблемости (вариации, изменения, разброса) результирующей переменной (результата Y), объясняемой колеблемостью учитываемых факторов:

,

где

- межгрупповая дисперсия (факторная дисперсия), отражающая влияние только учтенных факторов (Х) на колеблемость результата Y;

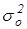- общая дисперсия, отражающая влияние всех факторов (как учтенных, так и не учтенных) на колеблемость результата Y.

Общая дисперсия:

,

где

- остаточная дисперсия, оценивающая колеблемость результата Y под влиянием всех неучтенных факторов.

В силу определения принимает значения от 0 до 1 ().

Если , то это означает, что регрессия ничего не дает.

Другой крайний случай означает точную подгонку: все точки наблюдений лежат на регрессионной линии, построенной по уравнению регрессии.

Чем ближе к 1 значение , тем лучше качество подгонки, тем аналитическое уравнение регрессии 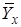более точно аппроксимирует Y.

Например, если 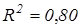, то колеблемость Y на 80% объясняется колеблемостью X.

При парной линейной регрессии коэффициент детерминации равен квадрату парного коэффициента корреляции: .

Недостаток коэффициента детерминации – его значение не отображает направление связи между исследуемыми переменными.

Дисперсия является важнейшей числовой характеристикой случайной величины. Она отражает степень «разброса» случайной величины относительно её математического ожидания (среднего значения).

Величину называют стандартной ошибкой, или стандартным отклонением случайной величины.

Стандартное отклонение показывает, насколько в среднем отклоняется случайная величина в совокупности наблюдений относительно своей средней (своего центра).

Если использовать обозначения:

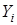- наблюдаемые значения Y при наблюдаемых значениях ;

- расчетные (по теоретическому уравнению регрессии) значения Y при наблюдаемых значениях ;

- среднее значение Y для данного массива наблюдений,

то дисперсии могут быть вычислены по следующим выражениям.

Общая дисперсия

(3.3)

Межгрупповая (факторная) дисперсия

(3.4)

Остаточная дисперсия

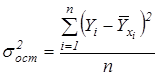(3.5)

Остаточная дисперсия рассчитывается через квадраты отклонений расчетных значений (определяемых по полученному аналитическому уравнению) от наблюдаемых значений.

Отобразим графически (рис.3.4).

Рис.3.4. К вопросу определения общей, межгрупповой и остаточной дисперсии

Внимание! “ n ” в формулах (3.3), (3.4), (3.5) должно быть обязательно одинаковым. Поэтому если при одном и том же в ходе наблюдений (в серии экспериментов) получено несколько значений Y, то расчетные значения Y необходимо вычислить при тех же столько раз, сколько в эксперименте, т.е. количество расчетных точек должно быть равно количеству наблюдаемых точек.

Данные для расчета дисперсии (пример 3.6):

i
	0, 1444	0, 16322	0, 00058
	0, 0529	0, 09181	0, 00533
	0, 0169	0, 00000	0, 01690
	0, 0144	0, 09181	0, 03349
	0, 3844	0, 16321	0, 04665
Σ	0, 6130	0, 51005	0, 10295

Тогда для примера 3.6 колеблемость Y объясняется колеблемостью X на 83, 2%, т.к.

.