Проверка линейной регрессионной модели с двумя переменными на адекватность по F-критерию Фишера

Коэффициент детерминации используется как критерий адекватности модели, т.к. является мерой объясняющей силы независимой переменной Х.

Если значение коэффициента детерминации близко к единице, то можно считать, что модель адекватна. Если его значение близко к нулю, то модель неадекватна, т.е. нет значимой линейной связи между зависимой и независимой переменными.

Но какой вывод можно сделать, если значение коэффициента детерминации имеет не явно выраженное граничное значение, например, 0, 5; 0, 45; 0, 44 и т.п.?

Понятно, что в таких случаях трудно сделать однозначный вывод о наличии связи, т.е. об адекватности построенной модели. Необходим другой критерий, который бы однозначно давал ответ на вопрос об адекватности построенной модели. Наиболее распространенным из таких критериев является критерий Фишера.

Для определения статистической значимости коэффициента детерминации проверяется нулевая гипотеза (случай отсутствия значимой линейной связи между X и Y) против гипотезы для F‑ статистики, рассчитываемой по формуле:

,

где

- число наблюдений;

- число оценённых параметров;

- число объясняющих переменных (факторов).

Это соотношение связывает - и F-статистики.

Если нулевая гипотеза справедлива, то значение F-статистики мало.

Не удивительно, что малым значениям F-статистики (отсутствие значимой функциональной связи X и Y) соответствуют малые значения (плохая аппроксимация данных).

Аппроксимация – это подбор для функции аналитического выражения, приближенно изображающего эту функцию.

F-тест Фишера.

Проверка модели на адекватность по F-критерию Фишера состоит из следующих этапов:

Этап 1. Рассчитываем F-статистику. Для парной регрессии F‑ статистика выглядит следующим образом:

.

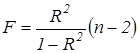Этап 2. Задаем уровень значимости α, которому соответствуют уровень возможной ошибки α ∙ 100%, уровень доверия (1-α)∙ 100% и уровень надежности (1-α).

Например, если мы считаем, что возможная ошибка α ∙ 100% для нас составляет 5%, это означает, что мы можем ошибиться не больше, чем в 5% случаев, а в 95% случаев (или в (1-α)∙ 100%) наши выводы будут правильными.

Этап 3. По статистическим таблицам F-распределения Фишера для выбранного уровня значимости и степеней свободы находим критическое значение , где – это степени свободы, связанные соответственно с дисперсией, которую можно объяснить из регрессионной модели, и с остаточной дисперсией.

Для парной регрессии: , где 1 – количество учитываемых в модели факторов; n – количество наблюдений; 2 – количество оцениваемых параметров .

Число степеней свободы показывает, сколько независимых элементов информации, которые образовались из элементов , необходимо для расчета соответствующей суммы квадратов.

Этап 4. Если , то мы отвергаем гипотезу о том, что (т.е. о том, что ), с риском ошибиться не больше, чем в α ∙ 100% случаев.

Поэтому, если , то при выбранном уровне доверия построенная нами регрессионная модель адекватна реальной действительности.