Проверка надежности оценок параметров линейной регрессионной модели с двумя переменными

Пусть у нас есть набор значений (набор данных, наблюдений) двух переменных , .

На самом деле, для одного и того же X мы можем наблюдать разные значения Y.

Пример 3.11. Если X – возраст работника, а Y – его зарплата, то работники одного возраста вполне реально могут иметь разную заработную плату.

Пример 3.12. Если X – доход семьи, а Y – расходы семьи на питание, то семьи с одинаковым доходом вполне реально могут расходовать на питание разные суммы.

Выбор состава и формулы связи переменных называется спецификацией модели (спецификацией уравнения регрессии).

Спецификация модели отражает наше представление о механизме зависимости Y от X и сам выбор объясняющей переменной X.

Например, Кейнсом была предложена следующая формула зависимости частного (индивидуального) потребления «С» от располагаемого дохода «»:

,

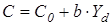где

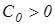- величина автономного потребления;

- предельная склонность к потреблению.

В данном случае выбрана линейная формула. Однако до тех пор, пока не оценены количественные значения параметров и b, не проверена надежность сделанных оценок, эта формула остается лишь гипотезой. Оценка значений параметров выбранной формулы статистической связи переменных называется параметризацией уравнения регрессии и производится методом наименьших квадратов.

Как же проверить надежность оценок параметров?

Запишем уравнение модели, отражающей зависимость от , в виде:

(3.6)

где

- значения переменных и ошибки в i -том наблюдении;

- неслучайная (детерминированная) величина;

- случайные величины;

- истинные значения параметров модели.

Уравнение (3.6) – это спецификация модели.

Какова природа ошибки ?

Обычно предполагают, что все возмущения, влияющие на объясняемую переменную и не учтенные явно в эконометрической модели, оказывают на объясняемую переменную некоторое результирующее воздействие, величина которого неизвестна заранее и связана со случайностью. Для её описания в модель добавляют (обычно аддитивным образом) случайную составляющую («Кси»), интегрирующую в себе влияние всех неучтенных явно в модели возмущений.

Наиболее существенные причины обязательного присутствия в моделях случайности следующие:

1. Невключение в модель всех объясняющих переменных.

Наша модель является упрощением действительности и на самом деле есть еще другие переменные (пропущенные переменные), от которых зависит Y.

Зарплата, например, может зависеть не только от возраста работника, но и от уровня образования работника, стажа работы, пола, типа фирмы (государственная, частная) и т.п.

Расходы на питание – не только от дохода семьи, но и от размера семьи, общего уровня цен, региона проживания и т.п.

2.Трудности в измерении данных (в данных присутствуют ошибки измерений).

Например, данные по расходам семьи на питание составляются на основании записей участников опросов, которые, как предполагается, тщательно фиксируют свои ежедневные расходы. Разумеется, при этом возможны ошибки.

3. Ограниченность объема статистических данных (ограниченность объема массива наблюдений).

Компонента является суммарным проявлением всех этих причин.

Таким образом, можно считать, что – случайная величина с некоторой функцией распределения, которой соответствует функция распределения случайной величины . Заметим, что оценки параметров модели, являясь функциями случайных наблюдений, также есть случайные величины.

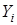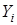Из оцененного по выборке уравнения регрессии предсказанное значение в точке (прогноз значения в точке ) составит:

,

где

- оценки истинных значений параметров , модели (3.6) (оценки параметров регрессии).

Остатки регрессии (отклонения теоретических значений от наблюдаемых) определяются из уравнения:

.

Не следует путать остаткирегрессии с ошибкамирегрессии в уравнении модели 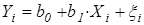. Разница состоит в том, что остатки , в отличие от ошибок , наблюдаемы.

Остатки регрессии – это наблюдаемые значения ошибок в уравнении модели.

Проверка надежности оценок параметров модели предполагает:

- проверку статистической значимости оценок параметров модели;

- определение доверительных интервалов для параметров модели.

t-тест Стьюдента для проверки на значимость оценок параметров регрессии, определенных методом наименьших квадратов

Можно показать, что оценки параметров, определенные методом наименьших квадратов, распределены по нормальному закону распределения.

Определим дисперсии оценок параметров регрессии.

Для этого необходимо знать дисперсию ошибок.

Но поскольку на практике, как правило, дисперсия ошибок неизвестна и оценивается по наблюдениям одновременно с оцениванием параметров регрессии , вместо дисперсии оценок мы можем получить лишь оценки дисперсии оценок .

1. Несмещенная оценка дисперсии ошибок:

,

где

- остатки регрессии (отклонения теоретических значений от наблюдаемых)

;

- i -тая точка на регрессионной прямой, которая отвечает наблюдаемому значению ;

n - размер выборки (количество наблюдений);

k - количество оцененных параметров (в случае парной регрессии 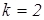, т.к. оценивается два параметра: и ).

2. Оценки дисперсии оценок параметров регрессии:

;

, (3.7)

где

- оценка дисперсии оценки ;

- оценка дисперсии оценки ;

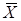- среднее по выборке значение X: .

Оценки стандартных отклонений (оценки стандартных ошибок) оценок параметров регрессии, которые приводятся в результатах регрессии в статистических пакетах, вычисляются на основе этих формул:

.

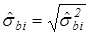Замечание. Предположим, что мы изучаем зависимость Y от X и число наблюдений n задано, но мы можем выбирать набор . Как выбрать так, чтобы точность оценки углового коэффициента была наибольшей? Оценка дисперсии оценки задается формулой (3.7), откуда видно, что чем больше , тем меньше величина оценки дисперсии . Поэтому желательно выбирать таким образом, чтобы их разброс вокруг среднего значения был большим.