Проверка выдвинутых гипотез.

Предположим, что верна гипотеза .

Тогда вероятность того, что t-статистика попала в интервал равна (1-α):

, (3.9)

где

- табличное критическое значение t-распределения Стьюдента с степенями свободы при заданном уровне значимости .

Следовательно, если значение t-статистики попадает в интервал , то вероятность этого события составляет .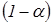

Например, при 40 степенях свободы и α =0, 05:

и в этом случае

.

Мы отвергаем гипотезу (и принимаем ) с 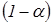∙ 100% -доверительным уровнем (при =0, 05 – с 95% -доверительным уровнем), если (“редкое” событие с точки зрения гипотезы ), в противном случае мы не можем отвергнуть (и принимаем ).

В эконометрике распространенной формой ноль-гипотезы является такая:

против альтернативной

.

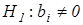В этом случае t-статистика для оценки i -того параметра принимает вид:

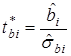(3.10)

Ее значение сравниваем с табличным критическим значением.

Для определения критического значения необходимо задать уровень значимости α. Затем по таблицам t-распределения Стьюдента при заданном уровне значимости и степенях свободы найти соответствующее критическое значение .

Если

,

мы можем сделать вывод о том, что с вероятностью (1-α) оценка является статистически незначимой (т.е. мы принимаем ноль-гипотезу ).

В противоположном случае, когда , с вероятностью (1-α) мы принимаем гипотезу 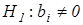и делаем вывод, что оценка является статистически значимой (статистически достоверно отличается от нуля).

Использованная t-статистика (3.10) является не чем иным, как отношением оценки к оценке её стандартного отклонения, или, иначе говоря, к оценке её среднеквадратического отклонения.

Отношения (3.10) называют t-значениями для оценок соответствующих параметров и приводятся всеми компьютерными пакетами в результатах регрессии. В частности, значение ( для 95% уровня доверия) позволяет сделать вывод об отличии от нуля (на соответствующем уровне доверия) коэффициента регрессии и, следовательно, о наличии влияния (связи) X и Y. Малые значения t-статистики соответствуют отсутствию достоверной статистической связи объясняющей переменной X и зависимой переменной Y.

Компьютерные пакеты приводят также P-значения (уровни значимости α) вычисленных t-статистик, т.е. вероятность того, что случайная величина, распределенная по закону , принимает значение по абсолютной величине большее, чем

.

Таким образом, P-значение – это показатель вероятности случайного значения оценки параметра регрессии, который сразу позволяет судить о значимости нулевой гипотезы для оценки параметра:

- если i -тое P-значение меньше принятого нами уровня значимости (обычно задают уровень значимости 0, 1; 0, 05 или 0, 01, что соответствует 10%, 5% или 1% уровню возможной ошибки), то делают вывод о неслучайной природе значения соответствующей оценки, т.е. о том, что оценка i -того параметра достоверна (статистически значима);

- в противном случае (если i -тое P-значение больше принятого нами уровня значимости) принимается гипотеза о случайной природе оценки соответствующего параметра регрессии, т.е. о её недостоверности (статистической незначимости). Это позволяет рассматривать фактор как неинформативный и ставить под сомнение необходимость включения его в модель.

Доверительные интервалы для параметров регрессии

Для того чтобы определить, как оценки параметров и связаны с истинными значениями параметров и , необходимо построить доверительные интервалы для параметров и регрессионной модели, т.е. такие интервалы, в которые с заданной вероятностью попадают их значения.

Разрешив неравенство в (3.9) относительно , получим

,

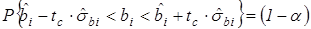т.е.

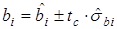
или

- (1-α)∙ 100%-доверительный интервал для (при α =0, 05 – 95% -доверительный интервал для ).

Доверительный интервал накрывает истинное значение параметра с заданной вероятностью.

Пример 3.13. Модель расходов семьи.

Пусть Х обозначает реальный доход семьи, Y – ее реальные расходы.

Для того чтобы исследовать зависимость расходов от доходов, была выполнена оценка параметров регрессии.

Количество наблюдений 122.

В скобках приведены оценки стандартных ошибок оценок параметров регрессии.

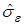- оценка стандартного отклонения остатков (оценка стандартной ошибки оценивания).

Соответствующие t-статистики равны

;

;

.

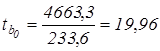Т.е. параметры статистически достоверно отличаются от нуля (параметры являются значимыми).

Доверительные интервалы для параметров:

;

.

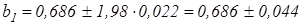Однако следует заметить, что значение коэффициента детерминации невелико.