Мета роботи

Вивчення й експериментальне визначення властивостей одновимірних функцій розподілу ймовірностей і густин імовірності випадкових процесів.

2 Ключові положення

2.1 Вважається, що процеси, які вивчаються, є стаціонарними й ергодичними. У таких процесів одновимірні функція розподілу ймовірностей і густина ймовірності не залежать від часу й їх можна визначити по одній реалізації.

2.2 За визначенням значення одновимірної функції розподілу ймовірностей F (x) дорівнює ймовірності того, що в довільний момент часу процес Х (t) набуде значення, яке не перевищує x:

F (x) = P { X (t) £ x }. (1)

Значення одновимірної густини ймовірності процесу р (х) дорівнює границі відношення ймовірності того, що в довільний момент часу процес X (t) набуде значення на інтервалі (x – D x /2, x + D x /2), до довжини інтервалу D x, коли D x ® 0:

. (2)

Функції f (x) і р (x) задовольняють ряду властивостей (табл. 1), які легко довести, користуючись їх визначеннями (1) і (2).

Таблиця 1 – Властивості функцій f (x) і р (x)

	р (x)	f (x)

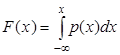
Функції f (x) і р (x) використовуються для обчислення ймовірностей попадання значень процесу в заданий інтервал (рядок 2 в табл. 1), а також для виконання статистичного усереднення при визначенні характеристик процесу або результату певної операції над випадковим процесом.

2.3 Для процесів, які часто зустрічаються, відомі аналітичні вирази функцій р (x) і f (x). Так, у нормального (гауссового) процесу (наприклад, флуктуаційної завади) густина ймовірності записується

(3)

де 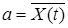– середнє значення або математичне сподівання випадкового процесу

; (4)

s – середньоквадратичне відхилення випадкового процесу, воно визначається як s = , де D [ X (t)] – дисперсія випадкового процесу – середнє значення квадрата відхилень значень випадкового процесу від його середнього значення

. (5)

Функція розподілу ймовірностей нормального процесу записується у різних підручниках та посібниках одним з наступних виразів:

(6)

де – форми запису інтегралів ймовірностей.

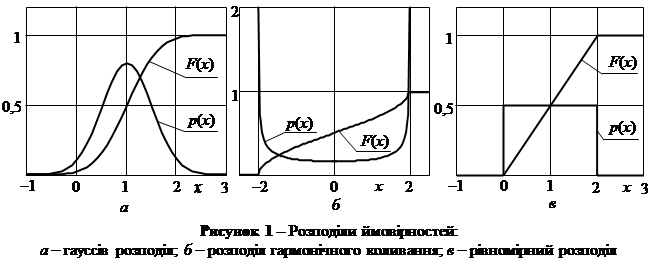
На рис. 1, а приведені графіки гауссового розподілу ймовірностей при а = 1 і s = 0, 5.

2.4 Розподіл імовірностей гармонічного коливання X (t) = A× cos(2p f t + j), де А і f – постійні величини, a j – випадкова величина, описується виразами:

(7)

Середнє значення гармонічного коливання дорівнює 0, а середньоквадратичне відхилення дорівнює . На рис. 1, б наведені графіки розподілу ймовірностей гармонічного коливання при А = 2. Коли х = А значення густини ймовірності прямує в ¥.

2.5 Зустрічаються також процеси з рівномірним розподілом на інтервалі (x _min, x _max). Розподіл описується виразами

(8)

Середнє значення процесу з рівномірним розподілом дорівнює (x _min + x _max)/2, а середньоквадратичне відхилення дорівнює . Графіки рівномірного розподілу ймовірностей при x _min = 0 і x _max = 2 наведені на рис. 1, в.

3 Ключові питання

3.1 Які процеси називаються стаціонарними, ергодичними?

3.2 Дати визначення одновимірної функції розподілу ймовірностей випадкового процесу і довести її властивості.

3.3 Дати визначення одновимірної густини ймовірностей випадкового процесу і довести її властивості.

3.4 Як знайти ймовірність попадання значень випадкового процесу в заданий інтервал, користуючись функцією розподілу ймовірностей або густиною ймовірностей?

3.5 Записати вираз для математичного сподівання і дисперсії випадкового процесу. Яка їх фізична суть?

3.6 Записати вираз для нормального розподілу ймовірностей і пояснити суть величин, що входять у вираз.

3.7 Пояснити вигляд графіків розподілу ймовірностей гармонічного коливання з випадковою фазою, флуктуаційного шуму і процесу з рівномірним розподілом.

3.8 Описати принцип дії пристрою для вимірювання функції розподілу ймовірностей і густини ймовірностей випадкового процесу.

4 Домашнє завдання

4.1 Вивчити розділ “Імовірнісні характеристики випадкових процесів” за конспектом лекцій і літературою [1, с. 136...157; 2, с. 109...118].

4.2 Виконати розрахунки і побудувати графіки функції розподілу ймовірностей і густини ймовірностей нормального випадкового процесу з середнімзначенням а = 0 і середньоквадратичним відхиленням s = 1 + 0, 1 N, де N – номер лабораторного стенда. Розрахунки провести для діапазону значень
– 3s < x < 3s. При відсутності таблиць інтегралів ймовірностей значення інтегралів можуть бути визначені за наближеними формулами:

Ф(z) @ 1 – 1, 3 exp[–0, 44(z + 0, 75)²] при z > 0;

Ф(z) = – Ф(| z |) при z < 0, Ф(0) = 0, Ф(¥) = 1;

Ф₀(z) @ 0, 5 – 0, 65 exp[–0, 44(z + 0, 75)²] при z > 0;

Ф₀(z) = – Ф₀(| z |) при z < 0, Ф₀(0) = 0, Ф₀(¥) = 0, 5;

V (z) @ 0, 65 exp[–0, 44(z + 0, 75)²] при z > 0;

V (z) = 1 – V (| z |) при z < 0, V (0) = 0, 5, V (¥) = 0.

Результати розрахунків оформити у вигляді таблиці і графіка.

4.3 Підготуватись до обговорення за ключовими питаннями.