Мета роботи. Вивчення методу експериментального визначення кореляційних характеристик випадкових процесів і детермінованих сигналів

Вивчення методу експериментального визначення кореляційних характеристик випадкових процесів і детермінованих сигналів. Дослідження зв’язку між кореляційними функціями і спектрами випадкових процесів і детермінованих сигналів.

2 Ключові положення

2.1 Кореляційною функцією (КФ) випадкового процесу X (t) називається математичне сподівання добутку значень процесу, які він набуває в моменти часу t ₁ і t ₂:

. (1)

Значення КФ K_Х (t ₁, t ₂) визначають величину статистичної залежності між значеннями процесу в моменти часу t ₁ і t ₂. У стаціонарних процесів значення КФ залежать не від вибору t ₁ і t ₂, а від відстані між ними t = t ₂ – t ₁, а КФ позначається K_X (t). Далі будемо розглядати лише стаціонарні процеси і вважати, що вони є ергодичні. Для ергодичних процесів КФ визначається

, (2)

де x (t) – реалізація процесу X (t).

2.2 Незалежно від вигляду КФ різних процесів, для них виконуються наступні властивості:

- K_X (0) = Р_Х, де Р_Х – середня потужність процесу;

- K_X (0) ³ K_X (t) – коли t = 0, значення функції K_X (t) максимальне;

- K_X (t) = K_X (–t) – функція K_X (t) парна;

- K_X (¥) ® 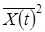, де – середнє значення процесу.

2.3 Чим менше значення K_X (t) порівняно з K_X (0), тим менша статистична залежність між значеннями процесу, які віддалені за часом на t. Якщо значення K_X (t) = 0, то значення процесу X (t), які віддалені за часом на такий інтервал t, є некорельованими. Значення K_X (t) і K_X (0) легше порівнювати, якщо перейти до нормованої кореляційної функції

. (3)

Значення R_X (0) = 1 і –1 £ R_X (t) £ 1.

2.4 Часто для опису кореляційних властивостей випадкових процесів замість КФ використовують число – інтервал кореляції t_к. Інтервал кореляції запроваджується для “грубого” опису кореляційних властивостей процесу, а саме, значення процесу, віддалені на час t > t_к, вважають некорельованими, а значення процесу, віддалені на час t £ t_к, вважають корельованими. Використовуються різні способи визначення інтервалу кореляції:

1) Інтервал кореляції t_к є основа прямокутника висоти K_X (0), площа якого дорівнює площі під кривою модуля КФ (рис. 1, а):

. (4)

2) Інтервалом кореляції є таке значення t_к, за якого при t > t_к значення КФ не перевищують деякого заданого рівня (рис. 1, б).

3) Якщо КФ має коливальний характер, то як інтервал кореляції t_к можна прийняти значення t, за якого КФ перший раз приймає нульове значення (рис. 1, в).

2.5 Виміряти КФ строго у відповідності з (2) неможливо, оскільки для цього необхідна реалізація процесу нескінченої тривалості. Можна виміряти КФ лише реалізації випадкового процесу скінченої тривалості. Очевидно, чим більша тривалість реалізації процесу Т _реал, тим точніше виміряна КФ реалізації відображає КФ процесу. Пристрій для вимірювання КФ реалізації називається корелометром (рис. 2). Тут час затримки t визначає аргумент вимірюваного значення КФ. Якщо корелометр, показаний на рис. 2, виконати на процесорі чи на комп’ютері, то можна отримати масив значень К_Х (kТ _д), де Т _д – інтервал ди-
скретизації реалізації процесу x (t); значення аргументу лежать у межах
– Т _реал £ kТ _д £ Т _реал. Отримані масиви значень kТ _д і К_Х (kТ _д) виводяться на двовимірний дисплей

2.6 Основною спектральною характеристикою випадкових процесів є спектральна густина потужності G_X (f), яка визначає розподіл потужності процесу за частотою. Кількісно функція G_X (f) визначає потужність процесу в смузі частот протяжністю 1 Гц біля частоти f. Теорема Вінера-Хінчина стверджує, що функції K_X (t) і G_X (w) пов’язані перетворенням Фур’є

(5)

Якщо функція G_X (f) відома, то за допомогою неї можна визначити середню потужність процесу

. (6)

Зокрема, якщо процес – квазібілий шум зі спектральною густиною потужності N ₀ у смузі частот (0, F _max),

P_X = N ₀× F _max. (7)

2.7 Часто досить знати ширину спектра процесу F _max. Ширина спектра випадкового процесу визначається за функцією G_X (f) такими ж самими методами, що і ширина спектра детермінованого сигналу. На рис. 3 показано, як ширина спектра визначається на заданому рівні у, тобто F _max є протяжність області частот, поза якою спектральна густина потужності процесу не перевищує значення у.

Оскільки функції K_X (t) і G_X (f) пов’язані перетворенням Фур’є, то є зв’язок між шириною спектра F _max і інтервалом кореляції t_к процесу:

t_к× F _max = 0, 5. (8)

Знак рівності у виразі (6) слід розуміти наступним чином – добуток інтервалу кореляції і ширини спектра процесу є величиною порядку 0, 5.

2.8 Кореляційна функція є також характеристикою детермінованого сигналу, хоча і немає такого тлумачення, як для випадкового процесу. КФ неперіодичного детермінованого сигналу визначається

, (9)

де T_s – тривалість сигналу s (t).

Виміряти КФ детермінованого сигналу можна за допомогою корелометра, наведеного на рис. 2, в якому інтегрування провадеться на інтервалі (0, T_s) і відсутній множник перед інтегралом.

Нехай s (t) – П-імпульс амплітуди А і тривалості T _ім

(10)

Після підстановки (10) в (9) отримаємо

(11)

КФ П-імпульсу показана на рис. 4, а.

Із виразу (9) випливає, що K_s (0) = E_s – енергія сигналу s (t). Перетворення Фур’є від K_s (t) дає квадрат амплітудного спектра (спектральну густину енергії) сигналу s (t). Перетворення Фур’є від виразу (11) дає квадрат відомого виразу для амплітудного спектра П-імпульсу

. (12)

2.9 Розглянемо радіоімпульс з П-подібною обвідною тривалості T _ім

(13)

де А, f ₀ і j₀ – амплітуда, частота і початкова фаза коливання.

Після підстановки (13) в (9) отримаємо

(14)

Із (14) випливає, що КФ радіоімпульсу є косинусоїда з нульовою початковою фазою і не залежить від фази радіоімпульсу. Тому, якщо початкова фаза радіоімпульсу j₀ є випадковою величиною, то КФ радіоімпульсу визначається формулою (14). Обвідна КФ радіоімпульсу збігається з КФ сигналу, який є обвідною радіоімпульсу. На рис. 4, б наведено КФ радіоімпульсу, побудовану за формулою (14) при f ₀ = 4/ T _iм.

Перетворення Фур’є від виразу (14) дає квадрат амплітудного спектра
сигналу (13)

. (15)

3 Ключові питання

3.1 Дати визначення КФ випадкового процесу.

3.2 Як визначається КФ ергодичного процесу?

3.3 Перелічити основні властивості КФ випадкового процесу.

3.4 Які параметри випадкового процесу можна визначити за його КФ?

3.5 Що стверджує теорема Вінера-Хінчина?

3.6 Перелічити способи визначення інтервалу кореляції.

3.7 Який зв’язок між шириною спектра й інтервалом кореляції випадкового процесу?

3.8 Який вигляд має КФ П-імпульсу?

3.9 Який вигляд має КФ радіоімпульсу з П-подібною обвідною?

3.10 Чому початкова фаза радіоімпульсу не впливає на його КФ?

4 Домашнє завдання

4.1 Вивчити розділ “Кореляційна теорія випадкових процесів” за конспектом лекцій і літературою [1, с. 73…79, 149...164; 2, с. 67…72, 109...118].

4.2 Побудувати структурні схеми корелометрів для дослідження кореляційних функцій випадкових процесів і детермінованих сигналів.

4.3 Розрахувати і побудувати графіки КФ П-імпульсу і радіоімпульсу з П-подібною обвідною за таких вихідних даних: тривалість імпульсів Т _ім = 2 мс, частота коливання радіоімпульсу f ₀ = 500× (N + 1) Гц, де N – номер лабораторного стенда. Для заданих імпульсів розрахувати і побудувати графіки спектрів за виразами (11) і (14).

4.4 Підготуватись до обговорення за ключовими питаннями.