
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Мета роботи. Дослідження характеристик випадкових процесів, перетворених нелінійним безінерційним колом: спектральної густини потужності й густини ймовірності.
|
|
Дослідження характеристик випадкових процесів, перетворених нелінійним безінерційним колом: спектральної густини потужності й густини ймовірності.
2 Ключові положення
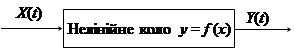 2.1 Під час дослідження проходження випадкових процесів через нелінійні безінерційні кола вважається, що відомо статистичні характеристики вхідного процесу X (t) та залежність у = f (x) між миттєвими значеннями вхідного і вихідного процесів. Необхідно знайти характеристики вихідного процесу Y (t).
2.1 Під час дослідження проходження випадкових процесів через нелінійні безінерційні кола вважається, що відомо статистичні характеристики вхідного процесу X (t) та залежність у = f (x) між миттєвими значеннями вхідного і вихідного процесів. Необхідно знайти характеристики вихідного процесу Y (t).
2.2 Найбільш розповсюдженою функцією f (x) для опису нелінійних перетворень є поліном степені n
f (x) = a 0 + a 1 x + a 2 x 2 +... + an xn, (1)
де a 0, a 1, a 2,..., an – коефіцієнти поліному.
Коефіцієнти і степінь поліному визначаються в результаті апроксимації характеристики реального електричного кола або виходячи з деяких припущень. Крім поліноміальної залежності (1) використовуються також кусково-лінійна залежність (односторонній, двосторонній обмежувач), експонентна залежність.
2.3 Кожний з доданків функції (1) вносить свій внесок у формування значень реакції нелінійного кола на дію. Так, a 0 описує появу постійної складової при х = 0; a 1 x – лінійний доданок, що забезпечує пропорційне відображення значень х в у; a 2 x 2 – квадратичний доданок, a 3 x 3 – кубічний доданок і т.д. забезпечують внески, пропорційні х 2, х 3 і т.д.
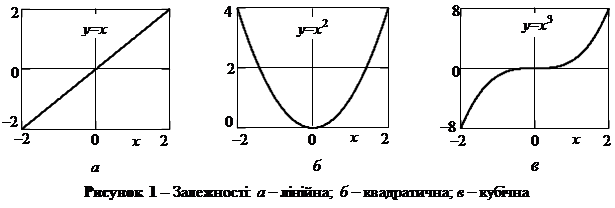
Залежності a 1 x, a 2 x 2 і a 3 x 3 при a 1 = a 2 = a 3 = 1 наведені на рис. 1.
 |

2.4 Найпростіша дія – гармонічне коливання x (t) = A 1cos2p f 1 t. У такому випадку
у (t) = a 0 + a 1 A 1cos2p f 1 t + a 2 A 12cos22p f 1 t +... + an A 1 n cos n 2p f 1 t. (2)
Якщо скористатися формулами кратного аргументу, то одержимо
y (t) = Y 0 + Y 1cos 2p f 1 t + Y 2cos2p2 f 1 t +... + Yn cos2p nf 1 t, (3)
де Y 0 – постійна складова реакції;
Y 1, Y 2,..., Yn – амплітуди першої, другої,..., n -ї гармонік реакцій.
Таким чином, реакція на гармонічну дію містить постійну складову і гармоніки частоти дії – це принципово відрізняє нелінійні кола від лінійних, в яких нові складові не виникають.
2.5 У випадку бігармонічної дії
x (t) = A 1cos2p f 1 t + A 2cos2p f 2 t. (4)
Підхід до визначення реакції такий самий, як і показаний вище – вираз для x (t) підставляється в поліном (1). При зведенні суми (4) у квадрат, куб і т.д. з’являться степені косинусоїд частот f 1 і f 2, що після перетворень дає вираз виду (3) для коливань частот f 1 і f 2. Але з’являються ще і добутки косинусоїд та їх степенів. Добуток косинусоїд призводить до появи складових сумарної і різницевої частот.
У загальному випадку будуть мати місце складові комбінаційних частот
f комб =½ pf 1 ± qf 2½, (5)
де p, q – цілі числа 0, 1, 2,..., але такі, що p + q £ n. Їх сума N = p + q називається порядком комбінаційної частоти.
Так, якщо n = 3, то у спектрі реакції можуть бути складові частот f 1, f 2, 2 f 1, 2 f 2, ½ f 1± f 2½, 3 f 1, 3 f 2, ½ 2 f 1 ± f 2½, ½ f 1 ± 2 f 2½. Амплітуди складових залежать від амплітуд А 1 і A 2 і коефіцієнтів поліному (1).
Для наочності наводять спектральну таблицю (табл. 1).
Таблиця 1 – Спектральна таблиця для n = 3
| Частоти складових вихідного коливання | Амплітуди складових вихідного коливання, які викликані окремими доданками поліному | ||
| a 1 x | a 2 x 2 | a 3 x 3 | |
| 0, 5 a 2(A 12 + A 22) | |||
| f 1 | a 1 A 1 | 1, 5 a 3 A 1(0, 5 A 12 + A 22) | |
| 2 f 1 | 0, 5 a 2 A 12 | ||
| 3 f 1 | 0, 25 a 3 A 13 | ||
| f 2 | a 1 A 2 | 1, 5 a 3 A 2(A 12 + 0, 5 A 22) | |
| 2 f 2 | 0, 5 a 2 A 22 | ||
| 3 f 2 | 0, 25 a 3 A 23 | ||
| ÷ f 1 ± f 2÷ | a 2 A 1 A 2 | ||
| ÷ 2 f 1 ± f 2÷ | 0, 75 a 3 A 12 A 2 | ||
| ÷ f 1 ± 2 f 2÷ | 0, 75 a 3 A 1 A 22 |
2.6 При проходженні випадкового процесу через нелінійне коло вид розподілу миттєвих значень істотно змінюється. Визначення густини ймовірності вихідного процесу розглянемо на прикладі проходження через нелінійність y = ax 2. Нехай X (t) має нормальний розподіл ймовірностей із нульовим середнім значенням
p (x) =  . (6)
. (6)
За такої нелінійності зв’язок між x і y неоднозначний: для першої області x 1 = +  і для другої області x 2 = –
і для другої області x 2 = –  . Для додатних значень Y (t)
. Для додатних значень Y (t)
p (y) =  (7)
(7)
Модуль похідної визначається  Від’ємні значення Y (t) не приймає. Після перетворень співвідношення (7) і з врахуванням зазначеного одержимо остаточний вираз
Від’ємні значення Y (t) не приймає. Після перетворень співвідношення (7) і з врахуванням зазначеного одержимо остаточний вираз
 (8)
(8)
На рис. 2 показано розподіл (8) при а = 1 і s Х = 1.
 Викладений підхід можна використовувати і при інших функціях y = f (x) і розподілах p (x).
Викладений підхід можна використовувати і при інших функціях y = f (x) і розподілах p (x).
2.7 Визначити спектральну густину потужності вихідного процесу GY (f) можна наступним способом: визначити спочатку кореляційну функцію вихідного процесу KY (t), а потім виконати над нею перетворення Фур’є. Виходячи із визначення кореляційної функції
 (9)
(9)
де f (x) – функція, що описує нелінійне коло;
р 2(х 1, х 2, t) – двовимірна густина ймовірності вхідного процесу.
В окремому випадку, коли у = ах 2, а вхідний процес гауссів з нульовим середнім, тобто
 , (10)
, (10)
де RX (t) – нормована кореляційна функція процесу X (t), то інтегрування (9) дає
 (11)
(11)
Якщо вхідний процес смуговий із середньою частотою f 0, то
KX (t) = kX (t)cos2p f 0t, (12)
де kX (t) – обвідна кореляційної функції процесу X (t).
Якщо до того ж процес вузькосмуговий, то

і
 (13)
(13)
Перетворення Фур’є від (13) дає: складову на нульовій частоті, низькочастотні складові, що примикають до нульової частоти і високочастотні складові навколо частоти 2 f 0.
Як випливає з пп. 2.4 і 2.5, при зведенні сигналу в квадрат спектр розширюється, тому що виникають другі гармоніки складових, і можна очікувати, що спектр функції  ширший, ніж D F /2, де D F – ширина спектра вхідного процесу. Тому ширина спектра низькочастотної складової вихідного процесу більша, ніж D F /2, а ширина спектра високочастотної складової більша, ніж D F.
ширший, ніж D F /2, де D F – ширина спектра вхідного процесу. Тому ширина спектра низькочастотної складової вихідного процесу більша, ніж D F /2, а ширина спектра високочастотної складової більша, ніж D F.
3 Ключові питання
3.1 У чому полягає задача дослідження проходження випадкових процесів через нелінійні кола?
3.2 Як описується нелінійне коло під час дослідження проходження процесів через нього? Наведіть приклади.
3.3 Описати спектр коливання на виході нелінійного кола при подачі до входу кола гармонічного коливання.
3.4 Описати спектр коливання на виході нелінійного кола при подачі до входу кола суми двох гармонічних коливань.
3.5 Від чого залежать амплітуди складових коливання на виході нелінійного кола при гармонічній чи бігармонічній дії на вході?
3.6 Що таке комбінаційні частоти?
3.7 Описати спосіб аналітичного визначення густини ймовірності на виході нелінійного безінерційного кола.
3.8 Описати спосіб аналітичного визначення спектральної густини потужності на виході нелінійного безінерційного кола.
4 Домашнє завдання
4.1 Вивчити розділ “Перетворення випадкових процесів нелінійними безінерційними колами” за конспектом лекцій і літературою [1, с. 220…230, 329…334; 2, розд. 11.1, 11.2, 11.4, 11.7].
4.2 На вхід нелінійного кола, що описаний поліномом третьої степені, подається бігармонічне коливання з частотами f 1 = 200 Гц і f 2 = 120 Гц та амплітудами А 1 = А 2 = 1 в. Розрахувати комбінаційні частоти f комб й їх амплітуди А комб в спектрі реакції, якщо коефіцієнти поліному a 0 = 0, a 1 = a 2 = a 3 = 1. Результати обчислень занести до табл. 2. Побудувати графік спектра реакції.
4.3 Підготуватись до обговорення за ключовими питаннями.
Таблиця 2 – Результати розрахунків комбінаційних частот
| N | p | q | f комб = pf 1 + qf 2 | f комб = ½ pf 1 – qf 2½ | ||
| f комб, Гц | А комб, В | f комб, Гц | А комб, В | |||