
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Мета роботи. Дослідження характеристик випадкових процесів на виході лінійного кола: спектральної густини потужності
|
|
Дослідження характеристик випадкових процесів на виході лінійного кола: спектральної густини потужності, функції кореляції, середньої потужності і густини ймовірності.
2 Ключові положення
 2.1 Під час дослідження проходження випадкових процесів через лінійні кола вважається, що відомі статистичні характеристики вхідного випадкового процесу x (t); відома також передавальна функція лінійного кола H (j w). Необхідно знайти характеристики вихідного процесу y (t).
2.1 Під час дослідження проходження випадкових процесів через лінійні кола вважається, що відомі статистичні характеристики вхідного випадкового процесу x (t); відома також передавальна функція лінійного кола H (j w). Необхідно знайти характеристики вихідного процесу y (t).
2.2 Спектральна густина потужності (СГП) процесу на виході лінійного кола зв’язана з СГП вхідного процесу через квадрат АЧХ кола
GY (w) = Gx (w) H 2(w). (1)
Зокрема, якщо вхідний процес – білий шум, то СГП вихідного процесу повторює квадрат АЧХ лінійного кола.
2.3 Кореляційна функція (КФ) процесу на виході лінійного кола визначається як перетворення Фур’є від СГП процесу
Ky (t) =  . (2)
. (2)
2.4 Нехай x (t) – білий шум з однобічною СГП Gx (f) = N 0, 0 £ f < ¥, подається до входу ідеального ФНЧ з АЧХ
H (f) =  (3)
(3)
де F зр – частота зрізу ФНЧ. Тоді СГП процесу y (t):
Gy (f) = Gx (f)× H 2(f) =  (4)
(4)
СГП процесу y (t) показана на рис 1, а.
Середня потужність процесу y (t):
Py =  =
=  = N 0
= N 0  F зр. (5)
F зр. (5)
Функція кореляції процесу y (t):
Ky (t) = N 0  F ср
F ср  . (6)
. (6)
На рис 1, б показана нормована функція кореляції RY (t) = KY (t)/ KY (0). Інтервал кореляції процесу y (t) tк = 1/(2 F зр).
 |
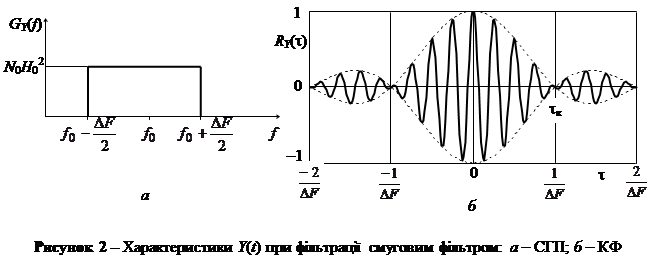
2.5 Нехай x (t) – білий шум з однобічною СГП Gx (f) = N 0, 0 £ f < ¥ подається до входу ідеального смугового фільтра з АЧХ
H (f) =  (7)
(7)
де D F – смуга пропускання фільтра. Тоді СГП процесу y (t):
Gy (f) = Gx (f)× H 2(f) =  (8)
(8)
СГП процесу y (t) показана на рис 2, а.
Середня потужність процесу y (t):
Py =  =
=  = N 0
= N 0  D F. (9)
D F. (9)
Кореляційна функція процесу y (t):
Ky (t) = N 0  D F
D F  (10)
(10)
На рис 2, б показана нормована КФ RY (t) = KY (t)/ KY (0) при f 0 = 4D F. Інтервал кореляції процесу y (t) tк = 1/D F.
2.6 Уводиться поняття шумової смуги лінійного кола. Шумова смуга кола дорівнює інтегралу від квадрата нормованої АЧХ кола
F ш =  , (11)
, (11)
де H max – максимальне значення АЧХ. В ідеального ФНЧ шумова смуга фільтра F ш = F зр, а в ідеального смугового фільтра – F ш = D F. Шумова смуга кола дозволяє легко визначити потужність процесу на виході кола, якщо до входу кола подається білий шум з однобічною спектральною потужністю N 0:
Py = N 0× F ш×  . (12)
. (12)
2.7 Відносно розподілу ймовірностей процесу при проходженні через лінійне коло відомо наступне. Якщо на вході лінійного кола процес гауссів, то вихідний процес також гауссів – вид розподілу не змінюється, змінюються тільки його параметри. Якщо на вході кола процес не гауссів, то вид розподілу змінюється, і вихідний процес має розподіл імовірностей більш близький до гауссового, ніж розподіл вхідного процесу.
2.8 Коло є вузькосмуговим, якщо його смуга пропускання значно менше ширини спектра вхідного процесу. У вузькосмугових колах має місце явище нормалізації процесу, яке полягає в наступному – незалежно від виду розподілу вхідного процесу, розподіл імовірностей процесу на виході вузькосмугового лінійного кола є гауссовим.
3 Ключові питання
3.1 У чому полягає задача проходження випадкових процесів через лінійні кола?
3.2 Як визначити спектральну густину потужності процесу на виході лінійного кола?
3.3 Як визначити кореляційну функцію процесу на виході лінійного кола?
3.4 Що таке шумова смуга лінійного кола?
3.5 У чому полягає практична корисність поняття “шумова смуга”?
3.6 Як змінюється вид розподілу імовірностей процесу при проходженні через лінійне коло?
3.7 Що таке вузькосмугове лінійне коло?
3.8 Що таке нормалізація процесу лінійним колом?
4 Домашнє завдання
4.1. Вивчити розділ “Перетворення випадкових процесів лінійними колами” за конспектом лекцій і літературою [1, с. 202 – 220; 2, с. 247 – 256].
4.2. Побудувати графік АЧХ ФНЧ Батерворта, яка описується виразом
 , де F зр – частота зрізу ФНЧ на рівні 0, 707, n – порядок фільтра. Прийняти, що F зр = 1000 Гц, а n дорівнює номеру лабораторного стенда. Знайти шумову смугу заданого ФНЧ. До входу ФНЧ подано білий шум з N 0 = 10–4 В2/Гц. Розрахувати потужність шуму на виході ФНЧ. Під час інтегрування скористатись табличним інтегралом
, де F зр – частота зрізу ФНЧ на рівні 0, 707, n – порядок фільтра. Прийняти, що F зр = 1000 Гц, а n дорівнює номеру лабораторного стенда. Знайти шумову смугу заданого ФНЧ. До входу ФНЧ подано білий шум з N 0 = 10–4 В2/Гц. Розрахувати потужність шуму на виході ФНЧ. Під час інтегрування скористатись табличним інтегралом  .
.
4.3. Підготуватись до обговорення за ключовими питаннями.