Опис лабораторного макета. Лабораторна робота виконується на комп’ютері в середовищі HP VEE з використанням віртуального макета

Лабораторна робота виконується на комп’ютері в середовищі HP VEE з використанням віртуального макета, структурну схему якого наведено на рис. 2. Макет надає можливість дослідити характеристики процесів з рівномірним розподілом ймовірностей, з гауссовим розподілом ймовірностей і гармо-
нічного коливання.

Для кожного із процесів макет реалізує дві основні функції:

1. Генерування N відліків досліджуваного процесу X (t) і виведення їх на дисплей “Реалізація процесу”.

2. Розрахунки на основі генерованих відліків значень і виведення на
дисплей:

а) функції розподілу ймовірностей;

б) густини ймовірності;

в) середнього значення;

г) середньоквадратичного відхилення (СКВ).

Для кожного досліджуваного процесу використовується свій спосіб генерування відліків, різні параметри процесів, якими вони задаються.

Генерування відліків процесу з рівномірним розподілом ймовірностей виконується за допомогою вбудованої функції randomize. Дослідник може установлювати значення x _min і x _max.

Генерування відліків процесу з гауссовим розподілом ймовірностей виконується за допомогою нелінійного перетворення двох масивів відліків u (i) і v (i) з рівномірним розподілом ймовірностей на інтервалі (0, 1), що отримуються за допомогою вбудованої функції randomize. Перетворення має вигляд

, (9)

де i – номер відліку в масиві;

а і s – середнє значення і середньоквадратичне відхилення досліджуваного випадкового процесу, які установлюються на макеті.

Генерування відліків гармонічного коливання виконується вбудованим функціональним генератором зі змінними амплітудою, частотою і початковою фазою коливання.

Розрахунок значень функції розподілу ймовірностей і густини ймовірності виконується в діапазоні значень аргументу від нижнього значення x _ниж до верхнього значення x _верх. Інтервал (x _ниж, x _верх) розбивається на М однакових
підінтервалів протяжністю D x = (x _верх – x _ниж)/ M; розраховується кількість відліків k_j, які попадають в j -й підінтервал (j приймає значення від 1 до М). Частота попадання значень відліків в j -й підінтервал q_j = k_j / N. При достатньо великих значеннях M і N (в макеті M = 200, N = 10000) значення частоти q_j дає ймовірність попадання значень відліків в j -й підінтервал. Відповідно до властивості густини ймовірності р (х) (рядок 1 в табл. 1) ймовірність попадання значень відліків в i -й підінтервал q_j = р (х_j)D x, де х_j = j D x. Тому

. (10)

Масиви значень р (х_j) і х_j виводяться на дисплей “Густина ймовірності”.

На основі властивості функції розподілу ймовірностей F (x), наведеної в рядку 5 табл. 1, розраховується масив значень

. (11)

Масиви значень F (х_j) і х_j виводяться на дисплей “Функція розподілуймовірностей”.

Розрахунок середнього значення досліджуваного процесу проводиться за формулою

, (12)

де X (i), – i -й відлік досліджуваного процесу. Число виводиться на дисплей “Виміряне середнє значення”.

Розрахунок середньоквадратичного відхилення досліджуваного процесу проводиться за формулою

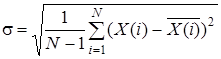. (13)

Число s виводиться на дисплей “Виміряне СКВ”.

7 Вимоги до звіту

7.1 Назва лабораторної роботи.

7.2 Мета роботи.

7.3 Результати виконання домашнього завдання.

7.4 Структурні схеми досліджень та результати виконання пп. 5.2…5.4 лабораторного завдання (графіки і числові значення).

7.5 Висновки за кожним пунктом завдання, в яких надати аналіз отриманих результатів (перевірка виконання властивостей функції розподілу ймовірностей і густини ймовірності, збіг експериментальних та теоретичних даних).

7.6 Дата, підпис студента, віза викладача з оцінкою за 100-бальною системою оцінювання.

Література

1 Баскаков С. И. Радиотехнические цепи и сигналы: Учебник для
вузов.– М.: Радио и связь, 1988 (1983).

2 Гоноровский И. С. Радиотехнические цепи и сигналы: Учебник для
вузов. – М.: Радио и связь, 1986 (1977).

Лабораторна робота 2.2
Кореляційні характеристики
випадкових процесів і детермінованих сигналів