
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Додаток а
|
|
Розрахунок кореляційної функції складного сигналу
Кореляційна функція неперіодичного сигналу тривалістю Ts визначається (для 0 £ t £ Ts)
Ks (t) = 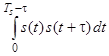 . (А.1)
. (А.1)
Розглянемо складний сигнал, що представляє собою послідовність П-імпульсів
s (t) =  , (А.2)
, (А.2)
де 1(t) – прямокутний імпульс амплітуди, що дорівнює 1, і тривалістю t0;
аi – коефіцієнти, що приймають значення +1 або –1;
n – число імпульсів у послідовності.
У сигналів, що складаються з П-імпульсів, кореляційна функція являє собою ламану лінію і для побудови її графіка достатньо розрахувати значення функції для t, що кратні t0. Після підстановки виразу (А.2) в (А.1) одержимо співвідношення, що визначає значення кореляційної функції сигналу (А.2) для значень t, що кратні t0
Ks (k t0) = 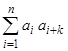 . (А.3)
. (А.3)
Тривалість сигналу Ts = n t0, тому необхідно розрахувати значення Ks (k t0) для
k = 0, 1, 2, …, n – 1, а Ks (n t0) = 0.
Для прикладу проведемо розрахунок кореляційної функції складного сигналу, побудованого на основі 7-елементного коду Баркера (n = 7): { ai } = +1, +1, +1, –1, –1, +1, –1. Обчислення за формулою (А.3) зводяться до наступного:
k = 0, Ks (0) = 7;
k = 1, Ks (t0) = 1× 1 + 1× 1 + 1× (–1) + (–1)× (–1) + (–1)× 1 + 1× (–1) = 0.
Аналогічно провадяться обчислення для k = 2, 3, 4, 5, 6. Результати розрахунку зведені в табл. А.1.
Таблиця А.1 – Результати розрахунку кореляційної функції
| k | ||||||||
| Ks (k t0) | –1 | –1 | –1 |
 Графік нормованої кореляційної функції розглянутого сигналу наведено на рис. А.1.
Графік нормованої кореляційної функції розглянутого сигналу наведено на рис. А.1.
Лабораторна робота 2.6
Дослідження проходження сигналів і шумів
через синхронний і частотний детектори