
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Рекуррентное уравнение динамики основного капитала
|
|
В среднесрочных и долгосрочных моделях развития предприятия и экономики страны в целом обязательно участвует уравнение, описывающее динамику капитальных ресурсов, т.е. ресурсов, участвующих в процессе производства, изменение их во времени с учетом возможных инвестиций и износа. При этом предполагается, что ежегодные отчисления (амортизация) составляют постоянную долю (процент) остаточной стоимости амортизирующегося основного капитала. Эта доля называется коэффициентом или нормой амортизации. Если норму амортизации обозначить через  , а величину основных фондов на начало
, а величину основных фондов на начало 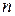 -го года через
-го года через 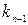 (
(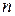 =1, 2, …), то получим рекуррентное уравнение при отсутствии инвестиций
=1, 2, …), то получим рекуррентное уравнение при отсутствии инвестиций
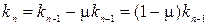 (
(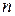 =1, 2, …).
=1, 2, …).
Если же мы хотим учесть возможные инвестиции, то уравнение изменится. Пусть 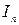 – объем инвестиций
– объем инвестиций 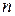 -го года. Тогда динамика капитала будет описываться рекуррентным уравнением
-го года. Тогда динамика капитала будет описываться рекуррентным уравнением
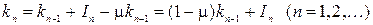 .
.
При этом начальное значение капитала 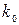 и объем инвестиций
и объем инвестиций 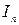 считаются известными. Предполагая, что существуют
считаются известными. Предполагая, что существуют 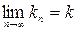 и
и 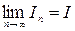 и переходя в этом уравнении к пределу при
и переходя в этом уравнении к пределу при 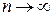 , получим предельную стоимость основного капитала
, получим предельную стоимость основного капитала  :
:
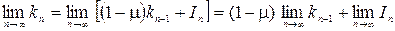 ,
,
или 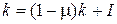 , т.е.
, т.е. 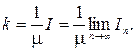
Пример
Найти остаточную стоимость основного капитала на начало 3-го года и предельную стоимость основного капитала, если  ,
, 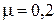 ,
, 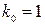 млн у.е.
млн у.е.
► Найдем объем инвестиций в первый год 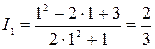 и стоимость основного капитала
и стоимость основного капитала  на начало второго года
на начало второго года
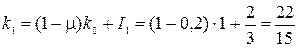 . Затем найдем
. Затем найдем 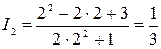 и стоимость основного капитала на начало третьего года
и стоимость основного капитала на начало третьего года
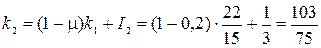 . Предельную стоимость основного капитала найдем по формуле
. Предельную стоимость основного капитала найдем по формуле 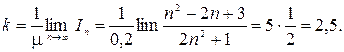 ◄
◄