
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Паутинообразная модель рынка
|
|
Рассмотрим простейшую динамическую модель рынка некоторого товара. В этой модели предполагается, что объем спроса в любой текущий момент времени 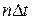 зависит от уровня цены этого периода –
зависит от уровня цены этого периода –  , а предложение реагирует на изменение цены с некоторым запаздыванием и зависит от уровня цены в предыдущем периоде –
, а предложение реагирует на изменение цены с некоторым запаздыванием и зависит от уровня цены в предыдущем периоде –  . Обозначим через
. Обозначим через  и
и  объемы спроса и предложения в период
объемы спроса и предложения в период 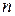 , тогда
, тогда  и
и  . Следующее предположение модели состоит в том, что изменение цены во времени происходит таким образом, что текущий спрос равняется текущему предложению, т.е.
. Следующее предположение модели состоит в том, что изменение цены во времени происходит таким образом, что текущий спрос равняется текущему предложению, т.е.  или
или  . Чтобы упростить анализ этого уравнения, предположим, что
. Чтобы упростить анализ этого уравнения, предположим, что
 .
.
Подставив эти выражения в уравнение  , получим уравнение
, получим уравнение  , которые вместе с равенствами
, которые вместе с равенствами  образует так называемую паутинообразную модель рынка. Предположим, что существуют
образует так называемую паутинообразную модель рынка. Предположим, что существуют  , тогда, переходя в последнем уравнении к пределу при
, тогда, переходя в последнем уравнении к пределу при 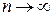 , получим
, получим  или
или  . Отсюда найдем
. Отсюда найдем  . Можно показать, что если
. Можно показать, что если  и существуют
и существуют  , то существует и
, то существует и  В этом случае
В этом случае  называется предельным значением равновесных цен
называется предельным значением равновесных цен  .
.
Пример
Найти предельное значение равновесных цен в паутинообразной модели рынка, если
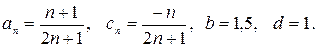
► Найдем  и
и  , т.к.
, т.к.  и
и  определены, то Þ
определены, то Þ  – предельное значение равновесных цен определено
– предельное значение равновесных цен определено 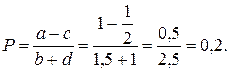 ◄
◄
ВОПРОСЫ ПРОМЕЖУТОЧНОГО КОНТРОЛЯ
1. Что называется действительным, комплексным числом?
2. Что называется действительной и мнимой частью, модулем и аргументом комплексного числа?
3. Что называется алгебраической, тригонометрической и показательной формами записи комплексного числа?
4. В каком случае два комплексных числа называются сопряженными?
5. По каким правилам производятся арифметические действия над комплексными числами? Напишите формулу Муавра.
6. Дайте определение функции. Что называется областью определения функции?
7. Каковы основные способы задания функции? Приведите примеры.
8. Какая функция называется периодической, четной, сложной? Приведите примеры.
9. Какие функции называются элементарными? Приведите примеры.
10. Сформулируйте определение предела последовательности, предела функции в точке и предела функции на бесконечности.
11. Как связано понятие предела функции с понятиями ее пределов слева и справа?
12. Сформулируйте определение ограниченной функции. Докажите теорему об ограниченности функции, имеющей предел.
13. Какая величина называется бесконечно малой и каковы ее основные свойства?
14. Какая величина называется бесконечно большой и какова ее связь с бесконечно малой?
15. Докажите основные теоремы о пределах функции?
16. Докажите первый и второй замечательный пределы.
17. Сформулируйте определение непрерывности функции в точке и на отрезке. Какие точки называются точками разрыва функции?
18. Сформулируйте основные свойства функций, непрерывных на отрезке, и дайте геометрическое истолкование этим свойствам.
19. Сформулируйте определение порядка одной бесконечно малой относительно другой бесконечно малой. Какие бесконечно малые называются эквивалентными. Сформулируйте их свойства. Приведите примеры.