
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Закрепления практических навыков
|
|
Задание 1. Представьте комплексные числа 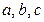 в тригонометрической, показательной формах и вычислить выражения
в тригонометрической, показательной формах и вычислить выражения  ,
,  . Ответ записать в алгебраической форме.
. Ответ записать в алгебраической форме.
1.  .
.
2.  .
.
3.  .
.
4. 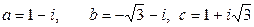 .
.
5.  .
.
6. 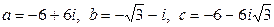 .
.
7.  .
.
8. 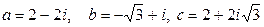 .
.
9. 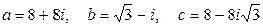 .
.
10. 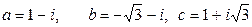 .
.
Задание 2. Для заданной последовательности  : а) найдите
: а) найдите  ; б) найдите
; б) найдите  такое, что для всех
такое, что для всех  выполняется неравенство
выполняется неравенство  .
.
1)  ; 2)
; 2)  ;
;
3)  ; 7)
; 7)  ;
;
4)  ; 8)
; 8)  ;
;
5)  ; 9)
; 9) 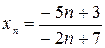 ;
;
6)  ; 10)
; 10)  .
.
Задание 3. Найти пределы функций, не пользуясь правилом Лопиталя
1. 1) 
 ; при x0=
; при x0= 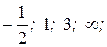 2)
2)  ;
;
3)  4)
4)  5)
5) 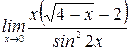 .
.
2. 1)  2)
2) 
3)  4)
4)  5)
5)  .
.
3. 1)  2)
2) 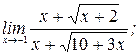
3) 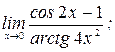 4)
4)  5)
5)  .
.
4. 1) 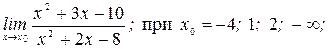 2)
2) 
3)  4)
4)  5)
5)  .
.
5. 1)  2)
2) 
3)  4)
4) 
5)  .
.
6. 1) 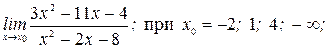 2)
2) 
3) 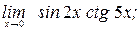 4)
4)  5)
5)  .
.
7. 1)  2)
2) 
3)  4)
4)  5)
5) 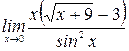 .
.
8. 1) 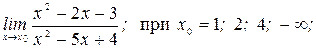 2)
2) 
3)  4)
4) 
5) 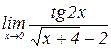 .
.
9. 1)  2)
2) 
3)  4)
4)  2)
2)  .
.
10. 1)  2)
2) 
3)  4)
4)  5)
5)  .
.
Задание 4. Заданы функция  и два значения аргумента
и два значения аргумента  и
и  . Требуется установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента, в случае разрыва найти пределы в точке разрыва справа и слева и сделать схематический чертёж функции вблизи точки разрыва.
. Требуется установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента, в случае разрыва найти пределы в точке разрыва справа и слева и сделать схематический чертёж функции вблизи точки разрыва.
1.  . .
| 2.  . .
|
3. 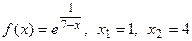 . .
| 4.  . .
|
5. 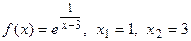 . .
| 6.  . .
|
7. 
| 8. 
|
9. 
| 10. 
|
Задание 5. Функция  задана различными аналитическими выражениями в различных областях изменения независимой переменной. Найти точки разрыва функции, если они существуют, и построить график функции.
задана различными аналитическими выражениями в различных областях изменения независимой переменной. Найти точки разрыва функции, если они существуют, и построить график функции.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 
|
Задание 6. Дайте определение непрерывности функции в точке. При каком значении  функция
функция  будет непрерывной в точке
будет непрерывной в точке 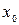 . Построй те график этой функции
. Построй те график этой функции
1.  2.
2. 
3. 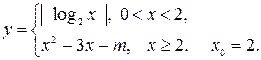 4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10.  .
.
Задание 7. 1. Исследуйте, будет ли функция  принимать значение равное 0, внутри отрезка [-1; 1].
принимать значение равное 0, внутри отрезка [-1; 1].
2.Исследуйте, будет ли функция  принимать значение равное 0, внутри отрезка [1; 3].
принимать значение равное 0, внутри отрезка [1; 3].
3. Исследуйте, будет ли уравнение  иметь корни принадлежащие отрезку [-2; 2].
иметь корни принадлежащие отрезку [-2; 2].
4. Исследуйте, будет ли уравнение 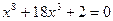 иметь корни принадлежащие отрезку [-1; 1].
иметь корни принадлежащие отрезку [-1; 1].
5. Исследуйте, будет ли функция  принимать значение равное 7, внутри отрезка [-2; 2].
принимать значение равное 7, внутри отрезка [-2; 2].
6. Исследуйте, будет ли функция  принимать значение
принимать значение  внутри отрезка [-2; 2].
внутри отрезка [-2; 2].
7. Исследуйте, будет ли уравнение  иметь корни принадлежащие отрезку [1; 2].
иметь корни принадлежащие отрезку [1; 2].
8. Исследуйте, будет ли уравнение  иметь корни принадлежащие отрезку [1; 2].
иметь корни принадлежащие отрезку [1; 2].
9. Исследуйте, будет ли функция  принимать значение равное 0, внутри отрезка [-2; 2].
принимать значение равное 0, внутри отрезка [-2; 2].
10. Исследуйте, будет ли функция 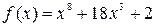 принимать значение равное нулю внутри отрезка [-1; 1].
принимать значение равное нулю внутри отрезка [-1; 1].
[1] Вейерштрасс Карл (1815 – 1897) – выдающийся немецкий математик.
[2] Больцано Бернард (1781 – 1848) – чешский математик, философ, логик.
[3] Коши Огюстен (1789 – 1857) – выдающийся французский математик.