
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение 2.4.
|
|
Статистика  называется исправленной выборочной дисперсией.
называется исправленной выборочной дисперсией.
Для доказательства состоятельности оценки  может быть использована теорема Хинчина и свойства сходимости по вероятности. Ранее было получено выражение для оценки
может быть использована теорема Хинчина и свойства сходимости по вероятности. Ранее было получено выражение для оценки  в виде:
в виде:
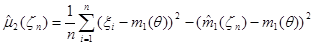
К совокупности случайных величин  применима теорема Хинчина: величины
применима теорема Хинчина: величины  независимы и имеют одинаковую функцию распределения (поскольку величины
независимы и имеют одинаковую функцию распределения (поскольку величины  образуют выборку), кроме того, математическое ожидание каждой величины
образуют выборку), кроме того, математическое ожидание каждой величины  конечно (по условию постановки исходной задачи, приведенной в начале пункта). Таким образом, по теореме Хинчина:
конечно (по условию постановки исходной задачи, приведенной в начале пункта). Таким образом, по теореме Хинчина:
 , при
, при 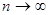 .
.
Оценка  является состоятельной, что по определению означает:
является состоятельной, что по определению означает:
 , при
, при 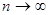
откуда по определению сходимости по вероятности
 , при
, при 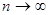 .
.
Функция возведения в квадрат является непрерывной, и, как и для всякой непрерывной функции, в силу свойства сходимости по вероятности:
 , при
, при 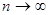 .
.
В силу свойства суммы двух пределов по вероятности,
 , при
, при 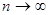 ,
,
откуда следует, что
 , при
, при 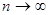 ,
,
то есть оценка  в соответствии с определением является состоятельной.
в соответствии с определением является состоятельной.
Для доказательства состоятельности оценки  могут быть использованы свойства сходимости по вероятности или утверждение 2.1.
могут быть использованы свойства сходимости по вероятности или утверждение 2.1.
В соответствии с определением оценки  :
:
 ,
,
где оценка  состоятельна, то есть
состоятельна, то есть  при
при 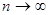 , и числовая последовательность
, и числовая последовательность  стремиться к 1 при
стремиться к 1 при 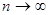 . Последнее означает, что для любого
. Последнее означает, что для любого  всегда можно найти
всегда можно найти  такое, что при
такое, что при 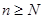 :
:
 ,
,
отсюда, считая элементы последовательности 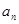 функциями
функциями  тождественно равные постоянным, получим:
тождественно равные постоянным, получим:
 ,
,
тогда, очевидно, что и для всякого 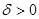 :
:
 .
.
Таким образом, числовая последовательность 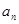 сходится по вероятности к 1 при
сходится по вероятности к 1 при 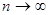 ,
,  . Оценка
. Оценка  , отсюда по свойству сходимости по вероятности:
, отсюда по свойству сходимости по вероятности:
 , при
, при 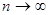 .
.
Поскольку статистика  является несмещенной оценкой
является несмещенной оценкой 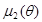 , то для проверки состоятельности статистики
, то для проверки состоятельности статистики  можно воспользоваться утверждением 2.1, для этого покажем, что дисперсия статистики
можно воспользоваться утверждением 2.1, для этого покажем, что дисперсия статистики  конечна и стремиться к нулю с ростом
конечна и стремиться к нулю с ростом 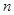 ,
,  при
при 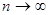 . При вычислении дисперсии
. При вычислении дисперсии  дополнительно потребуется существование четвертого центрального момента
дополнительно потребуется существование четвертого центрального момента  :
:
 ,
,
будем считать, что это требование выполнено.
Прежде всего, вычислим дисперсию 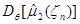 статистики
статистики  , которую, как было показано ранее, можно представить в следующем виде:
, которую, как было показано ранее, можно представить в следующем виде:
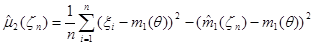 .
.
Далее, подставляя выражение для  получим:
получим:
 .
.
Введем центрированные случайные величины  , тогда для
, тогда для  получим выражение:
получим выражение:
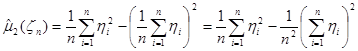
Теперь, возводя в квадрат и преобразовывая, получим выражение:
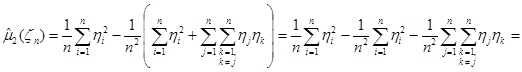
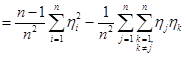 .
.
Представим дисперсию 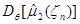 в виде:
в виде:
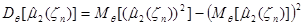
| (2.4) |
Вычислим  :
:
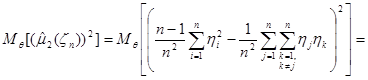
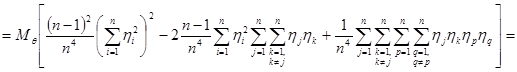
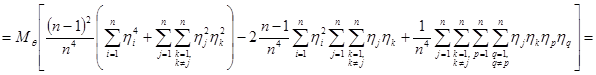
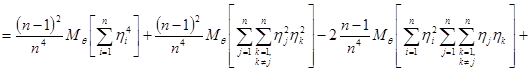
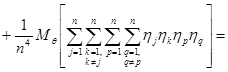
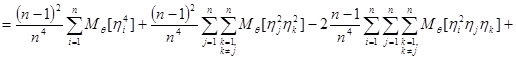
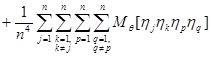 .
.
Заметим, что величины  (
(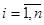 ) совместно независимы, поскольку независимы величины
) совместно независимы, поскольку независимы величины  (
(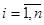 ), так как
), так как  образуют выборку, и кроме того:
образуют выборку, и кроме того:
 .
.
Рассмотрим слагаемые  в сумме
в сумме  , зафиксируем
, зафиксируем  , и рассмотрим все возможные варианты для индексов
, и рассмотрим все возможные варианты для индексов  и
и 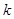 :
:
1)  ,
,
а)  – невозможно, поскольку
– невозможно, поскольку 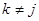 и
и  ;
;
а)  :
:
 ;
;
2)  ,
,
а)  :
:
 ;
;
б)  :
:
 .
.
Таким образом, все слагаемые  .
.
Рассмотрим слагаемые  в сумме
в сумме  , зафиксируем индексы
, зафиксируем индексы  и
и 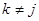 , и рассмотрим все возможные варианты для индексов
, и рассмотрим все возможные варианты для индексов  и
и  :
:
1)  :
:
а)  – невозможно, поскольку
– невозможно, поскольку  и
и  ;
;
б)  :
:
 ;
;
в) 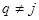 ,
,  :
:
 ;
;
2)  :
:
а)  :
:
 ;
;
б)  – невозможно, поскольку
– невозможно, поскольку  и
и  ;
;
в) 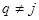 ,
,  :
:
 ;
;
3)  и
и  :
:
а)  :
:
 ;
;
б)  :
:
 ;
;
в) 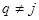 ,
,  :
:
 ;
;
Заметим, что только в случае 1б)  ,
,  и в случае 2а)
и в случае 2а)  ,
,  слагаемое
слагаемое  может быть отлично от нуля, во всех остальных случаях слагаемое
может быть отлично от нуля, во всех остальных случаях слагаемое  .
.
Таким образом, для  получим выражение:
получим выражение:
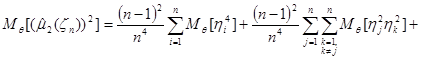
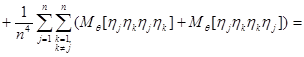

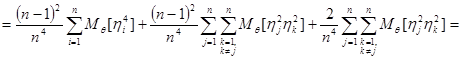
 .
.
Поскольку  , то
, то
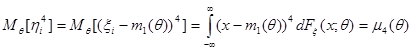
Поскольку величины  (
( ) независимы, то
) независимы, то  , тогда:
, тогда:
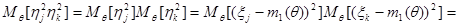
 .
.
Таким образом,
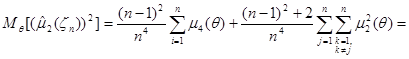
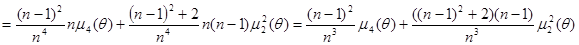 .
.
Из (2.4) с учетом (2.3) получим выражение для дисперсии 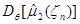 :
:
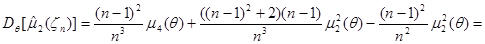
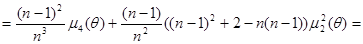
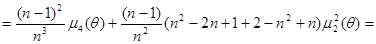
 .
.
Зная выражение для дисперсии 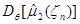 , легко вычислить дисперсию
, легко вычислить дисперсию  оценки
оценки  . Поскольку
. Поскольку  , то:
, то:
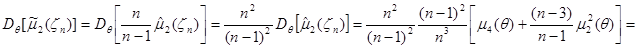
 .
.
Поскольку  и
и  , то очевидно
, то очевидно  и
и  , при
, при 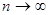 , откуда в силу утверждения 2.3 оценка
, откуда в силу утверждения 2.3 оценка  является состоятельной.
является состоятельной.