Определение 2.6.

Статистика называется выборочным центральным моментом 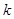-го порядка.

Легко видеть, что статистики являются несмещенными оценками , действительно:

.

Кроме того, если существует момент , то дисперсия статистики :

,

поскольку при в силу независимости и ,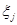

.

Таким образом,

.

Поскольку существует, то существует и , и с ростом 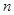, очевидно, дисперсия стремиться к нулю. Тогда в силу утверждения 2.1 (ранее было показано, что оценка является несмещенной) оценка является состоятельной.

Кроме того, можно показать ([1], параграф 1.3), что статистики являются асимптотически нормальными .

Исследование свойства несмещенности оценок сопряжено с определенными трудностями, тем не менее, достаточно легко убедиться в состоятельности оценок . Заметим, что статистики выражаются через статистики , где :

.

Таким образом, статистики являются непрерывными функциями от состоятельных оценок , которые сходятся по вероятности к значениям , отсюда в силу свойства сходимости по вероятности статистика сходится по вероятности к :

, при .

Заметим, что справа от предела стоит в точности :

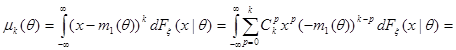
Таким образом, статистика сходится по вероятности к :

, при ,

отсюда статистика является состоятельной (по определению).