Следствие 3.5.

В условиях теоремы 3.4 равенство

имеет место тогда и только тогда, когда оценка и функция вклада связаны линейно, причем:

,

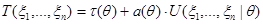где .

Доказательство:

1) Пусть выполнено равенство , тогда

,

поскольку по определению 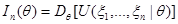. В пункте 3 доказательства теоремы 3.4 было показано, что

,

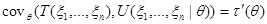тогда

.

Отсюда по свойству ковариации следует, что оценка и функция вклада связаны линейной зависимостью:

(3.4)

Вычисляя математическое ожидание левой и правой частей (3.4), получим:

.

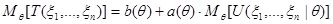В условиях теоремы 3.4 справедливы условия регулярности, при выполнении которых , тогда:

.

Статистика является несмещенной, то есть , тогда:

.

Вычисляя дисперсию левой и правой части (3.4), получим:

.

Поскольку по определению 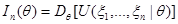, то и поскольку выполнено равенство , то . Таким образом,

,

где .

2) Пусть статистика и функция вклада связаны линейной зависимостью:

,

тогда по свойству ковариации:

.

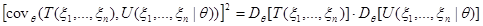В пункте 3 доказательства теоремы 3.4 было показано, что

,

отсюда,

,

тогда,

,

так как по определению .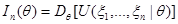

Поскольку статистика и функция вклада связаны линейно и выполнено равенство , то, как и в пункте доказательства 1, вычисляя математическое ожидание и дисперсию левой и правой части соотношения:

,

можно показать, что и .

Следствие доказано.