Определение 3.3. Пусть – вектор случайных величин и – функция вклада

Пусть 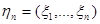– вектор случайных величин и – функция вклада. Функция

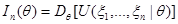
называется информацией Фишера о параметре , содержащейся в наблюдении .

Пусть – множество всех возможных значений случайного вектора 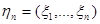и 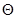– множество всех допустимых значений параметра , далее будем считать, что выполнены следующие условия, которые назовем условиями регулярности:

R1) Множество не зависит от параметра .

R2) На множестве функция правдоподобия положительна:

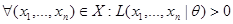
при всех .

R3) Функция правдоподобия дифференцируема по параметру при всех и всех .

R4) При всех справедливо равенство:

.

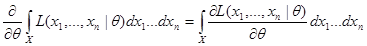R5) При всех существует момент :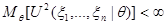

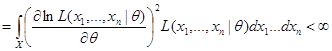
Теорема 3.4. (неравенство Рао-Крамера)

Пусть наблюдение представляет собой вектор случайных величин , – функция правдоподобия вектора , параметр , где 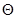– непустое множество допустимых значений параметра, – оценка величины . Если,

1) статистика является несмещенной оценкой величины ;

2) функция дифференцируема по при всех ;

3) выполнены условия регулярности R1-R5;

4) при всех существует производная:

;

тогда

,

где 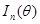информация Фишера о параметре , содержащаяся в наблюдении .