Определение 1.10.

Оценка называется состоятельной, если при каждом :

при .

Из свойства состоятельности, согласно определению сходимости по вероятности (приложение 1), следует, что для всяких и 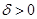можно найти такое, что при каждом :

.

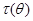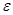Фактически это означает, что с увеличением объема выборки вероятность малого отклонения оценки от значения оказывается близкой к 1, то есть при больших с большой вероятностью (с вероятностью близкой к 1), значение окажется в -окрестности величины .

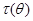Свойство состоятельности является обязательным свойством, оценки, не обладающие состоятельностью, не рассматриваются и не используются. Свойство несмещенности является желательным, более того, в некоторых случаях смещенные оценки оказываются «лучше» несмещенных, поэтому предпочтение отдают смещенным оценкам несмотря на отсутствие у них свойства несмещенности.

В некоторых случаях у оценки существует второй центральный момент (дисперсия) , который в общем случае зависит от значения параметра ,

.

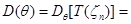
По величине дисперсии можно судить о мере «разброса» оценки : оценки с большим «разбросом» могут с большей вероятностью принимать значения далекие от оцениваемой величины 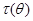, чем оценки с малым «разбросом». Кроме того, оценка с малым «разбросом» оказывается «сосредоточенной» вокруг математического ожидания , которое в случае дополнительного свойства несмещенности совпадает с оцениваемой величиной 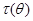, так что оценка фактически оказывается «сосредоточенной» вокруг величины 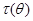. Отсюда следует, что предпочтение следует отдавать оценкам с малым «разбросом» (с малой величиной дисперсии).

Используя величины дисперсий оценок, можно сформулировать критерий наименьшей дисперсии сравнения оценок – «из двух оценок лучше та оценка, у которой дисперсия меньше».

Предположим, что есть класс несмещенных оценок величины 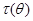с ограниченной дисперсией:

: , .

Пусть и две различных оценки из класса , в общем случае на основе дисперсий и не всегда удается указать, какая оценка «лучше», поскольку может оказаться (рисунок 1.2), что при одном значении параметра :

,

а при другом значении параметра наоборот:

.

В этом случае по принятому критерию наименьшей дисперсии невозможно указать, какая оценка лучше.

Рисунок 1.2. Дисперсии оценок.

Тем не менее, в некоторых случаях в классе есть оценка , которая при каждом значении параметра имеет наименьшую дисперсию среди дисперсий оценок класса (рисунок 1.3):

: .

В этом случае, оценка , очевидно, является наилучшей в классе и её следует признать оптимальной.

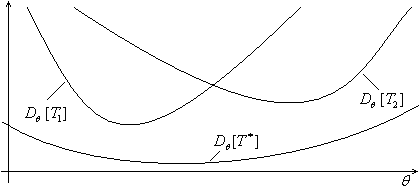
Рисунок 1.3. Дисперсия оптимальной оценки.