Определение 1.7.

Эмпирической функцией распределения называется случайная функция :

,

где функция 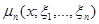равна количеству случайных величин выборки меньших .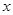

Теорема (сходимость по вероятности)

Пусть является эмпирической функцией распределения, построенной по выборке из распределения , тогда при всяком фиксированном случайная величина сходится по вероятности к при :

, при .

Теорема (равномерная сходимость по вероятности)

Пусть является эмпирической функцией распределения, построенной по выборке из распределения , тогда последовательность случайных величин 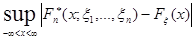сходится к нулю по вероятности при :

, при .

Теорема (Гливенко, сходимость с вероятностью 1)

Пусть является эмпирической функцией распределения, построенной по выборке из распределения , тогда последовательность случайных величин 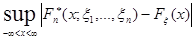сходится к нулю с вероятностью 1 («почти наверное») при :

, при .

Задача точечного оценивания неизвестных величин: параметров, вероятностей и моментов. Понятие статистики и оценки, свойства оценок: несмещенность и состоятельность. Сравнение несмещенных оценок на основе дисперсий. Понятие об оптимальной оценке, утверждение о единственности оптимальной несмещенной оценки (без доказательства). Обобщение критерия сравнения оценок на основе дисперсий с использованием среднеквадратичного отклонения, функции потерь и функции условного риска.