Определение 4.2.

Пусть – наблюдение и – функция правдоподобия. Оценка , доставляющая наибольшее значение функции правдоподобия при каждом наблюдении 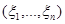, называется оценкой максимального правдоподобия (кратко, МП-оценкой):

.

Определение 4.2 следует понимать в следующем смысле: при каждом фиксированном элементарном событии , случайные величины наблюдения , …, принимают определенные числовые значения , а само наблюдение при фиксированном становится числовым вектором 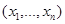. Для заданного вектора 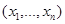согласно определению 4.2 вычисляется значение МП-оценки :

.

Тем самым для каждого задан способ вычисления МП-оценки , который и определяет функцию наблюдения . Таким образом, МП-оценка как функция наблюдения является статистикой.

Если при каждой реализации вектора наибольшее значение функции правдоподобия соответствует внутренней точке множества допустимых значений параметра 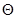и функция правдоподобия дифференцируема по параметру, то из необходимого условия экстремума следует равенство частных производных функции правдоподобия нулю в точке МП-оценки :

, .

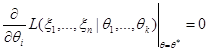Решение приведенной системы не всегда оказывается удобным, поэтому при выполнении определенных условий задачу нахождения наибольшего значения функции правдоподобия заменяют задачей нахождения наибольшего значения логарифма функции правдоподобия , поскольку логарифм функция монотонно возрастающая (и, следовательно, наибольшему значению логарифма функции правдоподобия будет соответствовать наибольшее значение самой функции правдоподобия):

, .

В случае скалярного параметра представленное уравнение имеет название уравнения правдоподобия.