Определение 6.5.

Статистикой критерия называется всякая статистика , отвечающая требованиям:

а) статистика отражает меру расхождения между наблюдаемым значением некоторой величины, вычисляемой на основе наблюдения, и гипотетическим (ожидаемым) значением некоторой, возможно уже другой, величины;

б) статистика имеет полностью известную функцию распределения (во многих случаях это требование может быть ослаблено: достаточно располагать способом приближенного вычисления значений функции распределения ).

Требование б) оказывается вполне естественным, поскольку гипотеза предписывает наблюдению некоторую определенную, возможно с точностью до параметров, функцию распределения. Статистика 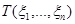устроена таким образом, что гипотеза предписывает статистике 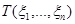полностью определенную функцию распределения (уже не зависящую от параметров). Вопрос лишь в том, удается ли найти выражение для функции распределения , если этого сделать не удается, то допустимым является нахождение выражения, аппроксимирующего функцию распределения , и в частности, нахождение предельной функции распределения, то есть функции распределения, к которой асимптотически с ростом стремится функция распределения .

В примере, рассмотренном выше, роль статистики играет модуль разности наблюдаемого количества выпавших гербов и гипотетического (ожидаемого) среднего количества выпадений герба при подбрасываниях в том случае, когда основная гипотеза верна:

.

Требование а) для статистики выполнено – статистика измеряет отклонение между наблюдаемой величиной и ожидаемым средним . Требование б) для статистики также выполнено, поскольку случайная величина имеет распределение Бернулли , параметры которого полностью определяются гипотезой (на это указывает значение вероятности 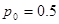), и следовательно функция распределения 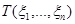полностью определена.

Пусть – множество всех возможных значений статистики :

.

Выделим в подмножество , которое отвечает «большим» значениям статистики (в примере, разобранном выше, подмножество имеет вид: 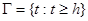, где некоторый порог). Будем считать, что если статистика принимает значение из множества , то наблюдение не согласуется с гипотезой, то есть гипотеза отклоняется, в противном случае наблюдение не противоречит гипотезе и гипотеза принимается.

Рисунок 6.1.Статистика критерия и критическая область.