
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определённый интеграл
|
|
Определение. Криволинейной трапецией называется плоская фигура, ограниченная сверху графиком функции  , снизу отрезком [ a, b ] оси ОХ и двумя прямыми х=а и х=b, параллельными оси ОУ.
, снизу отрезком [ a, b ] оси ОХ и двумя прямыми х=а и х=b, параллельными оси ОУ.
Рассмотрим задачу о вычислении площади криволинейной трапеции, ограниченной сверху графиком функции  , которая непрерывна и неотрицательна на отрезке [ a, b ]. Выполним следующие построения:
, которая непрерывна и неотрицательна на отрезке [ a, b ]. Выполним следующие построения:
1. Основание трапеции разобьём точками 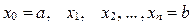 на n произвольных частей и обозначим длины отрезков
на n произвольных частей и обозначим длины отрезков 
2. Из точек разбиения восстановим перпендикуляры и через  обозначим площадь трапеции с основанием
обозначим площадь трапеции с основанием  Тогда площадь криволинейной трапеции
Тогда площадь криволинейной трапеции 
3. Внутри каждого отрезка  возьмём произвольную точку С i и вычислим в ней значение функции
возьмём произвольную точку С i и вычислим в ней значение функции  Площадь каждой из трапеций будет приближённо равна площади прямоугольника со сторонами
Площадь каждой из трапеций будет приближённо равна площади прямоугольника со сторонами  и
и  Тогда
Тогда
 (5)
(5)
Отметим, что сумма в правой части равенства (5)  называется интегральной суммой для функции
называется интегральной суммой для функции  на отрезке [ a, b ].
на отрезке [ a, b ].
4. Обозначим  длину наибольшего из отрезков разбиений
длину наибольшего из отрезков разбиений  , т.е.,
, т.е.,  В равенстве (5) перейдём к пределу при
В равенстве (5) перейдём к пределу при  и получим:
и получим:
 (6)
(6)
Таким образом, вычисление площади криволинейной трапеции свелось к вычислению предела интегральной суммы для функции  .
.
Определение. Если существует предел при  всех интегральных сумм, составленных для функции
всех интегральных сумм, составленных для функции  на отрезке [ a, b ], не зависящий ни от способа разбиения [ a, b ] на части, ни от выбора произвольной точки внутри каждого отрезка, то этот предел называется определённым интегралом от функции
на отрезке [ a, b ], не зависящий ни от способа разбиения [ a, b ] на части, ни от выбора произвольной точки внутри каждого отрезка, то этот предел называется определённым интегралом от функции  на отрезке [ a, b ]. Обозначается определённый интеграл
на отрезке [ a, b ]. Обозначается определённый интеграл
 (7)
(7)
где а называется нижним пределом, а b — верхним пределом.
Сравнивая формулы (6) и (7), получаем геометрический смысл определённого интеграла: определённый интеграл от неотрицательной функции  равен площади криволинейной трапеции с основанием [ a, b ] и ограниченной сверху графиком функции
равен площади криволинейной трапеции с основанием [ a, b ] и ограниченной сверху графиком функции  , т.е.
, т.е. 
Теорема (существования определённого интеграла). Если функция  непрерывна на отрезке [ a, b ], то существует определённый интеграл от этой функции на отрезке [ a, b ].
непрерывна на отрезке [ a, b ], то существует определённый интеграл от этой функции на отрезке [ a, b ].