
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА
|
|
Теорема (о производной от интеграла с переменным верхним пределом). Производная от определённого интеграла с переменным верхним пределом равна значению подынтегральной функции на этом верхнем пределе:

Доказательство:
Обозначим  Придадим переменной х приращение
Придадим переменной х приращение  тогда
тогда  получит приращение:
получит приращение: 
 где с – некоторая точка между х и
где с – некоторая точка между х и  По определению производной
По определению производной 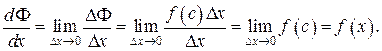
Следствие.  первообразная для функции
первообразная для функции  .
.
Теорема (формула Ньютона-Лейбница). Если функция  непрерывна на отрезке [ a, b ], то справедлива формула
непрерывна на отрезке [ a, b ], то справедлива формула
 (8)
(8)
где  любая первообразная для функции
любая первообразная для функции  , т.е.,
, т.е., 
Доказательство:
По следствию из предыдущей теоремы  первообразная для функции
первообразная для функции  . По теореме о первообразной для данной функции любая другая первообразная
. По теореме о первообразной для данной функции любая другая первообразная  отличается от
отличается от  на постоянное слагаемое:
на постоянное слагаемое:
 При
При  получим
получим  (по свойству 2 определённого интеграла).Следовательно,
(по свойству 2 определённого интеграла).Следовательно,  и
и  При
При 

Пример. Вычислить определённый интеграл 