Общие сведения. Антагонистические игры, которые рассматривались в предыдущих главах книги, описывают конфликты частного вида

Антагонистические игры, которые рассматривались в предыдущих главах книги, описывают конфликты частного вида, которые не всегда адекватны разным ситуациям или вообще не могут считаться приемлемыми.

В частности, антагонистические игры не затрагивают конфликты с числом игроков больше двух. Более того, даже в конфликтах с двумя игроками интересы сторон не всегда противоположны. Во многих конфликтах одна из ситуаций может оказаться предпочтительнее другой для обоих игроков.

Бескоалиционные игры являются играми более общей природы. Бескоалиционность понимается в том смысле, что группам игроков (“коалициям”) не приписывается ни каких-либо интересов, за исключением тех, которые вытекают из интересов отдельных игроков. Целью каждого игрока в такой игре является только получение, по возможности, индивидуального наибольшего выигрыша.

Определение 1. Бескоалиционной игрой называется игра N игроков (N ³ 2), каждый из которых имеет множество стратегий 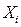, с функцией выигрыша Н_i (x), , где x Î C – ситуация, задаваемая на множество C декартового произведения стратегий C_і.

Определение 2. Бескоалиционная игра называется игрой с постоянной суммой, если существует такое постоянное С, что 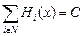, для всех ситуаций x Î C.

Класс антагонистических игр является классом игр двух лиц с нулевой суммой.

Определение 3. Конечная бескоалиционная игра двух игроков с ненулевой суммой называется биматричной игрой.

Как и в случае антагонистических игр, необходимо выработать принципы оптимального поведения игроков в бескоалиционных играх и найти решения (оптимальные стратегии каждого из игроков).

Для класса антагонистических игр принципом оптимальности является принцип максимина. В общих бескоалиционных играх возможны ситуации одновременного увеличения выигрышей всех игроков или хотя бы их одновременного выигрыша, поэтому в этих играх необходимо ввести формализованное описание таких понятий, как выгодность, устойчивость и справедливость того или иного решения игры.

Определение 4. Ситуация х в игре называется приемлемой для игрока і, если для любой его стратегии

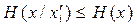, (3.39)

т.е. при применении і -м игроком в данной ситуации всех других стратегий, его выигрыш не может увеличиться.

Определение 5. Ситуация в игре, приемлемая для всех игроков, называется ситуацией равновесия по Нэшу (равновесной ситуацией).

Иными словами, ситуация х называется равновесной, если для любого игрока і Î N выполняется условие (3.39).

Из определения видно, что ни один из игроков не заинтересован в отклонении от своей стратегии, образующих в совокупности ситуацию равновесия.

В случае антагонистической игры приемлемые стратегии игроков совпадают с их оптимальными стратегиями. Для неантагонистических игр понятие оптимальной стратегии может вообще не иметь смысла: в таких играх оптимальными оказываются не стратегии отдельных игроков, а их сочетания для всех игроков сразу. В бескоалиционных играх как оптимальные следует квалифицировать не действия того или иного игрока, а совокупность действий всех игроков.

Поэтому в бескоалиционной игре решение игры – это чаще нахождение ситуаций равновесия.

Пример 1. Игра “Семейный спор”

Одна из наиболее распространенных интерпретаций игры следующая. Муж (первый игрок) и жена (второй игрок) могут выбрать одно из двух вечерних развлечений: футбольный матч или балет. Естественно предположить, что муж предпочтет футбол, а жена – балет. Однако для обоих гораздо важнее идти вместе, чем смотреть предпочитаемое зрелище в одиночестве. В данной 2´ 2 биматричной 2´ 2 игре функции выигрышей Н ₁ и Н ₂ соответственного первого и второго игроков можно представить в виде

и ,

где стратегии игрока 1: А ₁ – выбираю футбол; А ₂ – иду на балет;

игрока 2: В ₁ – иду на футбол, В ₂ – на балет.

Очевидно, что для первого игрока предпочтительнее ситуация (А ₁, В ₁), а для второго (А ₂, В ₂), и эти ситуации являются равновесными. Однако в данном примере, как будет показано ниже, есть еще и третья ситуация равновесия, состоящая в выборе игроками смешанных стратегий

;

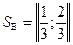
с ценой игры для обоих игроков .

Однако выигрыши каждого из игроков в этой ситуации равновесия меньше, чем в двух первых ситуациях равновесия, где они равны 2 или 1, в зависимости от ситуации и игрока.

Хотя стратегии (А ₁, В ₁) и (А ₂, В ₂) являются оптимальными, поскольку дают максимальные выигрыши, однако приносят игрокам неодинаковые выигрыши, поэтому не являются справедливыми.

Отметим также, что если в матричной игре ни одному из игроков не выгодно информировать противника о своей стратегии, то в данной биматричной игре это свойство не выполняется.

Действительно, если игроки не общаются до игры и оба обладают твердыми характерами, т.е. первый игрок выбирает стратегию А ₁, а второй – В ₂, то в результате они оба проигрывают. Аналогичная ситуация получится и в том случае, когда каждый из игроков имеет мягкий характер и решает уступить.Так сочетание устойчивости со справедливостью вступает в противоречие с сочетанием устойчивости и выгодности.

Лучшим для игроков в рассматриваемой игре является договорный вариант (А ₁, В ₁) или (А ₂, В ₂), причем справедливым решением будет их выбор одного из этих вариантов путем бросания монеты. Выпадение “герба” будет означать, например, что семейство идет на матч по футболу, а “решки” – на балет. Заметим, что в антагонистической игре в отличие от биматричной нет смысла вести переговоры до игры и уславливаться о совместном плане действий. В рассматриваемой игре ясно, что если игроки договорились бы играть оба, скажем, первую чистую стратегию, причем игрок 1 за получение большего выигрыша, чем игрок 2, заплатил бы ему 1/2, то решение было бы выгодным и справедливым для обоих игроков. Однако в рамках бескоалиционных игр такого рода дележи не предусматриваются.