
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение биматричных игр
|
|
Рассмотрим вначале биматричную игру 2´ 2 с матрицами выигрышей


соответственно игроков 1 и 2. Как и в случае матричных игр, смешанные стратегии полностью описываются вероятностями p и q выбора игроками своих первых чистых стратегий (вторые чистые стратегии выбираются, очевидно, с вероятностями 1- p и 1- q).
Опишем порознь множество приемлемых ситуаций, для каждого из игроков и изобразим эти множества на единичном квадрате p, q, где p Î [0, 1] и q Î [0, 1].
Начнем с описания ситуаций, приемлемых в игре для игрока 1.
Приемлемость ситуации (X, Y) для игрока 1 в биматричной игре означает, что
 , (3.43)
, (3.43)
 , (3.44)
, (3.44)
где А 1 и А 2 – вектор-строки, соответствующие первой и второй строке матрицы А, соответственно.
Подчеркнем, что эти условия приемлемости никак не связаны с матрицей В выигрышей игрока 2. Поэтому они будут совпадать с аналогичными условиями матричной игры с платежной матрицей А.
Приемлемость ситуации (X, Y) для игрока 2 означает, что
 (3.45)
(3.45)
 (3.46)
(3.46)
где В 1 и В 2 – вектор-столбцы, соответствующие первому и второму столбцу матрицы В соответственно.
В общем случае, Х =| p, 1 – p |. Рассмотрим три случая:
а) р = 1, (Х =|1, 0|). Тогда выражение (3.43) превращается в тождественное равенство, а условием приемлемости данной ситуации для игрока 1 оказывается неравенство (3.44). Для рассматриваемого случая его можно записать как
 ; (3.47)
; (3.47)
б) р = 0 (Х =|1, 0|). В этом случае выражение (3.44) превращается в тождественное равенство, а условием приемлемости данной ситуации для игрока 2 оказывается неравенство (3.43). Для рассматриваемого случая оно имеет вид
 ; (3.48)
; (3.48)
в) 0< р < 1 (Х =| p, 1 – p |). В этом случае оба неравенства (3.43) и (3.45) превращаются в равенство, и условием приемлемости становится
 . (3.49)
. (3.49)
Опишем ситуации приемлемости (3.47), (3.48) и (3.49) в развернутом виде. Так как

то соотношения (3.47), (3.48) и (3.49) можно соответственно записать как
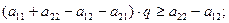 (3.50)
(3.50)
 (3.51)
(3.51)
 (3.52)
(3.52)
Таким образом, приемлемые для игрока 1 ситуации (X, Y) могут быть одного из трех типов:
(1, q), где  (3.53)
(3.53)
(0, q), где  (3.54)
(3.54)
(p, q), где  (3.55)
(3.55)
Неравенства (3.53) и (3.54) верны в случае, если
а 11 + а 22 – а 12 – а 21 > 0. Если а 11 + а 22 – а 12 – а 21 < 0, знак неравенства в соотношениях (3.53) и (3.54) необходимо поменять на противоположный.
Если величина а 11 + а 22 – а 12 – а 21 = 0, а а 22 – а 12 ¹ 0, выражение (3.55) не будет иметь место, поэтому будет выполняться или (3.53), или (3.54) и притом со знаком строгого неравенства.
Если же а 11 + а 22 – а 12 – а 21 = 0 и а 22 – а 12 = 0, все условия (3.53), (3.54) и (3.55) выполняются тождественно, и все ситуации будут приемлемыми для игрока 1.
Описание ситуаций приемлемости в развернутом виде для игрока 2 получаем аналогично из неравенств (3.45) и (3.46).
В общем случае Y =| q, 1– q |. Для трёх случаев получаем:
а) q = 1 (Y =|1, 0|). В этом случае приемлемость ситуации (X, Y) равносильна неравенству
 , (3.56)
, (3.56)
в развернутом виде

 . (3.57)
. (3.57)
б) q = 0 (Y =|0, 1|). В этом случае приемлемость ситуации (X, Y) определяется неравенством
 (3.58)
(3.58)
в развернутом виде
 . (3.59)
. (3.59)
в) 0< q < 1 (Y = | q, 1– q |). Условие приемлемости
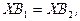 (3.60)
(3.60)
в развернутом виде
 . (3.61)
. (3.61)
Таким образом, приемлемые для игрока 2 ситуации (X, Y) могут быть одного из трех типов:
(p, 1), где  (3.62)
(3.62)
(p, 0), где  (3.63)
(3.63)
(p, q), где  (3.64)
(3.64)
Вновь подчеркнем, что неравенства (3.62) и (3.63) справедливы, если их знаменатель больше нуля. Если b 11 + b 22 – b 12 – b 21 < 0, то знак неравенства в выражениях (3.62) и (3.63) необходимо поменять на противоположный.
Для определения ситуаций, приемлемых одновременно как для первого, так и для второго игроков, удобно все найденные приемлемые ситуации представить на единичном квадрате (рис. 3.23).

Рис.3.23. Приемлемые ситуации для игроков 1 и 2
Для случаев, когда а 11 + а 22 – а 12 – а 21 ¹ 0 и b 11 + b 22 – b 12 – b 21 ¹ 0, приемлемые ситуации игроков 1 и 2 составляют трехзвенные зигзаги. Причем ситуации равновесия в смешанных стратегиях игрока 2 совпадают с поведением игрока 2 в матричной игре с матрицей выигрыша А, а поведение игрока 1 – с поведением игрока 1 в матричной игре с матрицей выигрышей В.
Таким образом, описанное равновесное поведение игроков оказывается ориентированным не столько на максимализацию собственного выигрыша, сколько на минимизацию выигрыша противника. Так “антагонизм поведения” может возникнуть и при отсутствии “антагонизма интересов”.
В приведенном на рис. 3.23 решении игры три ситуации равновесия соответствуют точкам R 1, R 2, R 3.
Если бы зигзаги приемлемых ситуаций были одинаковой ориентации, как показано на рис. 3.24, то пересечение приемлемых ситуаций игрока 1 и игрока 2 состояло бы из одной точки R.

Рис. 3.24. Нахождение ситуаций оптимальных по Нэшу
При решении биматричных игр большей размерности необходимо решать большую систему линейных неравенств, определяемых выражениями (3.43), (3.44) и (3.45), (3.46), а затем таким же конечно-рациональным путем находить точки пересечения приемлемых ситуаций игрока 1 и игрока 2. Причем любая конечная бескоалиционная игра имеет конечное и нечетное чисто ситуаций равновесия (решений игры). Поиск ситуаций равновесия в этом случае следует осуществлять с применением ПЭВМ.