
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математическая модель задачи принятия решений в условиях неопределенности состояний среды
|
|
Пусть субъект риска имеет в своем распоряжении n стратегий – х 1, х 2,... хn. Каждая стратегия может осуществиться в стохастически неопределенной обстановке, относительно которой можно лишь сделать m предположений. Эти предположения s 1, s 2,..., sm будет рассматривать как состояние среды или стратегии природы. Каждой стратегии субъекта риска и каждому возможному состоянию среды соответствует результат (исход) aij, определяющий выигрыш (или потери) субъекта риска.
Таким образом, имеет матрицу исходов:
| s 1 | s 2 | sm | ||
| х 1 | а 11 | а 12 | ... | а 1 m |
| х 2 | a 21 | a 22 | ... | a 2 m |
| ... | ... | ... | ... | |
| хn | an 1 | an 2 | ... | anm |
Задача заключается в определении такой стратегии, которая обеспечила бы субъекту риска наибольшую полезность.
Пример. Фермер может засеять поле тремя видами семян, (стратегии Хi, i = 1, 2, 3). Урожайность и, соответственно, прибыль аij зависят от климатических условий. Год может быть засушливым (состояние среды S 1); нормальным (S 2) или дождливым (S 3). В зависимости от ситуации (Хi, Sj), і =1, 2, 3; ј = 1, 2, 3, платежная матрица (матрица прибыли фермера) имеет вид
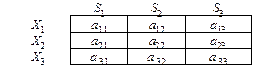 ,
,
где aij измеряются, например, в тыс. грн.
Фермеру могут быть известны вероятности (или их оценки) q 1,..., qm, с которыми природа реализует свои состояния, но он может их и не знать.
В отличие от теории игр, в данной игровой модели субъекту риска никто не противодействует, но элемент неопределенности состояния среды налицо. Игрок В в данной игровой модели – природа, " поведение" которой неизвестно, но во всяком случае не злонамеренно, как в модели матричных игр.
Казалось бы, отсутствие противостоящего разумного противника упрощает задачу выбора решения. Оказывается, нет: не упрощает, а усложняет. Правда, принимающему решение в " игре с природой" в самом деле, легче добиться большего успеха (ведь ему никто сознательно не мешает.), чем в игре с сознательным противником, но ему труднее обосновать свой выбор стратегии. В игре против сознательного противника элемент неопределенности снимается тем, что мы думаем за противника, " принимаем" за него решение, самое неблагоприятное для нас самих. В игре же с природой такая концепция не подходит: кто её знает, как она, природа, себя поведет.
Из сказанного вытекает следующие особенности рассматриваемой модели:
1) как и в теории стратегических игр ЛПР (игрок А) может отбросить все свои чистые стратегии (решения), которые являются дублирующими и доминируемыми, но исключать из рассмотрения состояния (стратегии) среды, которые соответствуют дублирующим и доминирующим стратегиям Sј (назовем условно стратегии игрока В) нельзя, поскольку эти состояния реализовываются независимо от того, выгодны они игроку В или нет;
2) решение ищется только для ЛПР (игрока А), поскольку среда (природа) наши рекомендации не воспринимает и ведет себя совершенно независимо от решений игрока А;
3) при принятии решений в условиях неопределенности состояний среды смешанные стратегии или не улучшают выигрыш игрока А или не всегда их можно реализовать для реальных ситуаций. Во всяком случае, смешанные стратегии имеют смысл только при многократном повторении решения, а в стратегических играх теория строилась из предпосылки, что игра (решение) может осуществляться и один раз;
4) поскольку природа (игрок В) не противостоит ЛПР, то, казалось бы, в этом случае решение найти проще, чем в случае стратегических игр. В действительности принятие решений в условиях неопределенности состояний среды сложнее из-за трудностей выбора критерия оптимальности решения, большой неопределенности в поведение среды (игрока В).
Как будет показано ниже, различные критерии оптимальности при этом часто дают различные решения. Все это обуславливает субъективный риск для принимающего решение, так как ЛПР субъективно выбирает различные критерии оптимальности.
При нахождении оптимального решения может быть использована не только оценочная матрица выигрышей |aij|, но и получаемая из нее матрица рисков |rji|:
rij = max aij – aij = b j – aij, (4.1)
где  – максимальный выигрыш в столбце j.
– максимальный выигрыш в столбце j.
В соответствии с соотношением (4.1) каждый элемент матрицы решений | aij | вычитается из наибольшего элемента max aij соответствующего столбца. Таким образом, величина риска интерпретируется как " плата (потери) за незнания состояния среды": если бы ЛПР знало истинное состояние среды Sј, оно бы выбрало стратегию, соответствующую максимальному выигрышу. Разница между наилучшим результатом для каждого Sј,  и получаемых при других решениях и есть мера риска.
и получаемых при других решениях и есть мера риска.
Пример. Построить матрицу рисков для матрицы выигрышей вида:
| S 1 | S 2 | S 3 | |
| Х 1 | |||
| Х 2 | |||
| Х 3 | |||
| Х 4 | |||
| Х 5 |
Решение. В начале упростим данную матрицу выигрышей. Напомним, что стратегия (решение) Хi является доминирующей над стратегией (решением) Хj, если все элементы матрицы выигрышей, соответствующие этой стратегии, не меньше элементов матрицы выигрышей, соответствующих стратегии Хj, а хотя бы один больше. В этом случае стратегия Хj называется доминируемой стратегией. Если все элементы, соответствующие стратегии Хi, равны всем соответствующим элементам матрицы выигрышей для стратегии Хj, то стратегии Хi и Хj называются дублирующими.
Так как решения (чистые стратегии) Х 1и Х 4являются дублирующими, а стратегия Х 5доминируется стратегией Х 1, то исключим из дальнейшего рассмотрения стратегии Х 4и Х 5. Получаем следующую матрицу выигрышей:
| S 1 | S 2 | S 3 | |
| Х 1 | |||
| Х 2 | |||
| Х 3 |
Произведем пересчет этой матрицы выигрышей в матрицу рисков.
Находим b j,  :
:



Рассчитаем элементы матрицы рисков:





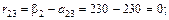



Таким образом, матрица рисков имеет вид:
| S 1 | S 2 | S 3 | |
| Х 1 | |||
| Х 2 | |||
| Х 3 |
Элементы матрицы рисков, соответствующие различным стратегиям, характеризуют общую неблагоприятность для субъекта риска отдельных состояний природы.
В рассмотренном выше примере состояние природы S 1 особенно неблагоприятно для стратегии Х 3 (r 31 = 150). Чем меньше величина риска rij, тем удачнее выбрано решение Хi при данном состоянии среды Sj. Очевидно, что если бы субъект риска знал, какое будет состояние среды Sj, то выбрал бы решение, при которой его выигрыш максимален, а при этом решении соответствующий риск rij равен нулю.
Если исходная оценочная матрица | bij | является матрицей проигрышей (убытков, негативных результатов для ЛПР), то элементы матрицы рисков определяются по формуле:
rij = bij – min aij . (4.2)
В этом случае количественной мерой риска выступает разница между результатом, который получает ЛПР при различных стратегиях и наилучшим результатом для данного состояния среды.
Пример. Построить матрицу риска для случая, когда оценочная матрица является для ЛПР матрицей проигрышей:
| s 1 | s 2 | ||
| х 1 | |||
| х 2 |
Решение. Используя выражение (4.2), получаем матрицу рисков:
| s 1 | s 2 | ||
| Х 1 | |||
| х 2 |
Принятие решения представляет собой выбор одного решения Х opt из конечного множества возможных решений Х 1,..., Хn. Выбор оптимального решения производиться по некоторому критерию оптимальности
Х opt = { Хk Î Х Ç ak = max  }. (4.3)
}. (4.3)
Выражение (4.3) читается следующим образом: в качестве оптимального выбирается то решение Хk, принадлежащее множеству возможных решений Х, для которого оценка a является лучшей из всех оценок решений  . Знак Ç означает совместное выполнение условий Хk Î Х и ak = max
. Знак Ç означает совместное выполнение условий Хk Î Х и ak = max  . Получение оценок ak и выбор оптимального решения в соответствии с выражением (4.3) в общем случае может быть неоднозначным. Но в экономических задачах выбор одного из нескольких хороших решений уже не создает трудностей.
. Получение оценок ak и выбор оптимального решения в соответствии с выражением (4.3) в общем случае может быть неоднозначным. Но в экономических задачах выбор одного из нескольких хороших решений уже не создает трудностей.
Для принятия решений в условиях неопределенности состояния среды могут применяться следующие критерии:
1) критерий недостаточного обоснования Лапласа;
2) максиминный критерий Вальда (критерий пессимизма);
3) минимаксный критерий Сэвиджа (критерий пессимизма, но с использованием матрицы рисков);
4) критерий пессимизма-оптимизма Гурвица;
5) производный критерий Ходжа-Лемона;
6) критерий Гермейера и др.