Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критерий минимаксного риска Сэвиджа. Этот критерий, также как и критерий Вальда, является критерием крайнего пессимизма, но при выборе оптимальной стратегии по критерию Сэвиджа ориентируются не
|
|
Этот критерий, также как и критерий Вальда, является критерием крайнего пессимизма, но при выборе оптимальной стратегии по критерию Сэвиджа ориентируются не на матрицу выигрышей или потерь, а на матрицу риска.
По критерию минимаксного риска Сэвиджа в качестве оптимальной выбирается та стратегия, при которой величина риска в наихудших условиях минимальна:
{ хk Î Х Ç 
}. (4.8.)
Сущность такого подхода состоит в том, чтобы всячески избегать большого риска при принятии решения. В смысле “пессимизма” критерий Сэвиджа сходен с критерием Вальда, но “пессимизм” здесь понимается по-другому.
Перерасчет матрицы выигрышей в матрицу рисков рассмотрен выше. Если же дана матрица потерь, то в этом случае элементы матрицы риска rij определяются следующим образом:
rij = bij – a j , (4.9.)
где bij – элементы матрицы потерь;
a j = 
bij – минимальные потери в столбце j.
Для рассмотренной в параграфе 4.2.2. матрицы потерь пересчитанная матрица рисков имеет вид:
| s 1 | s 2 | ||
| Х 1 | |||
| х 2 |
В соответствии с критерием Сэвиджа:
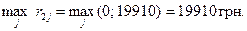
Тогда 
,
что соответствует стратегии х 1.
Как видим, в этом случае, в отличие от критерия Лапласа, минимаксный критерий, примененный к матрице потерь, и минимаксный критерий, примененный к матрице рисков, вычисленной по матрице потерь, дали различные решения.
Рекомендации. Критерий Сэвиджа следует применять при следующих обстоятельствах:
- о вероятностях различных состояний среды qj ничего не известно;
- необходимо исключить получение результата худшего, чем min max rij;
- результат min max rij устраивает ЛПР.
Как и в случае использования критерия Вальда, по критерию Сэвиджа также можно найти оптимальную смешанную стратегию S, которая минимизирует максимальное среднее значение риска, вычисленное для каждого состояния среды:
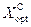= { хk Î Х Ç rk = max 
}.
Оптимальная смешанная стратегия S ищется в соответствии с теорией матричных игр.