
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критерий Лапласа. Этот критерий опирается на принцип недостаточного обоснования
|
|
Этот критерий опирается на принцип недостаточного обоснования. Поскольку вероятности состояния природы qj, 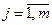 неизвестны, и ни одно состояние нельзя предпочесть другому, то исходя из принципа недостаточного обоснования, предполагается, что эти вероятности равны:
неизвестны, и ни одно состояние нельзя предпочесть другому, то исходя из принципа недостаточного обоснования, предполагается, что эти вероятности равны:
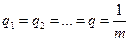 .
.
В этом случае, задача сводится к принятию решения в условиях стохастической определенности риска, которая рассматривалась в главе 2.
В частности, по критерию максимальной ожидаемой прибыли, будет применяться та стратегия хi, для которой максимальна величина
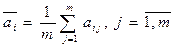 . (4.4)
. (4.4)
Если же используется критерий минимального ожидаемого риска, то будет применяться та стратегия хi, для которой минимальна величина
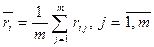 . (4.5)
. (4.5)
Покажем, что применение критериев максимума среднего выигрыша и минимума среднего риска для одних и тех же исходных данных приводит к одному и тому же результату.
Действительно, так как
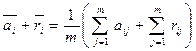 ,
,
а rij = b j – aij, то получаем, что 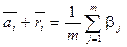 .
.
Для данной матрицы 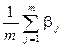 есть величина постоянная, поэтому
есть величина постоянная, поэтому
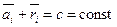 .
.
Из этого выражения видно, что если  отражается в максимум, то
отражается в максимум, то  принимает минимальное значение. Следовательно, оптимальная стратегия, полученная при применении максимизации среднего выигрыша, будет совпадать с оптимальной стратегией, полученной по критерию минимизации среднего риска.
принимает минимальное значение. Следовательно, оптимальная стратегия, полученная при применении максимизации среднего выигрыша, будет совпадать с оптимальной стратегией, полученной по критерию минимизации среднего риска.
Данное свойство справедливо и для случая, когда состояния природы неравновероятны.
Когда неопределённость в состояниях среды удаётся ослабить (например, на основе статистических наблюдений становятся известны оценки вероятностей qj, 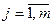 ), то в качестве критерия оптимальности выбирают критерий Байеса:
), то в качестве критерия оптимальности выбирают критерий Байеса:
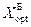 = { хk Î Х Ç ak = max
= { хk Î Х Ç ak = max  }, 4.6)
}, 4.6)
где ak = max  – максимальное математическое ожидание выигрышей.
– максимальное математическое ожидание выигрышей.
Отметим еще то важное положение, что в играх с природой при использовании критерия Лапласа и Байеса субъекту риска нет смысла применять смешанную стратегию S, которая представляют собой случайную величину на множестве чистых стратегий субъекта риска
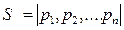 .
.
Если в игре против сознательного противника смешанные стратегию вводят его в заблуждение, то в игре против " равнодушной" природы этой резон отпадает. Действительно, если субъект риска применит смешанную стратегию, то его средний выигрыш, осредненный, как по состояниям среды, так и по применяемым стратегиям, будет равен
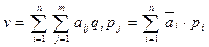 .
.
Но этот выигрыш не может быть больше максимальной из усредняемых величин, т.е. цена игры 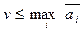 .
.
Отсюда и следует, что применение в игрес природой любой смешанной стратегии S, найденной по критерию Лапласа или Байеса, не может быть выгоднее для субъекта риска, чем применение оптимальной по этим критериям чистой стратегии.
Пример. Предприятие, должно определить объем услуг, чтобы удовлетворить клиентов в течение предстоящих праздников. Точное число клиентов не известно, но ожидается, что оно может принять одно из четырех значений: 200; 250; 300 или 350.
Для каждого из этих возможных значений существует наилучший уровень предложения (с точки зрения возможных затрат). Отклонения от этих уровней приводит к дополнительным затратам либо из-за превышения предложения над спросом, либо из-за неполного удовлетворения спроса.
Ниже приводится таблица, определяющая потери в тысячах гривен. Необходимо принять решение об уровне предложений хi, i = 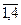 .
.
Клиенты
| S 1 | S 2 | S 3 | S 4 | |
| х1 | ||||
| х2 | ||||
| х3 | ||||
| х4 |
Решение. Принцип недостаточного обоснования предполагает, что ожидаемое значение числа клиентов имеет равномерный закон распределения с вероятностями
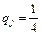 ,
, 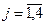 .
.
Ожидаемые средние потери при различных стратегиях предприятия равны
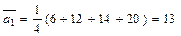 тыс. грн.;
тыс. грн.;
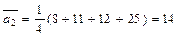 тыс. грн.;
тыс. грн.;
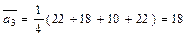 тыс. грн.;
тыс. грн.;
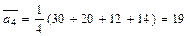 тыс. грн.;
тыс. грн.;
Таким образом, наилучшей стратегией в соответствии с критерием Лапласа будет стратегия х 1.
Рекомендации. Критерии Лапласа и Байеса следует использовать при достаточно большом числе реализаций оптимального решения. При этом среднее значение стабилизируется и мало отличается от математического ожидания этой случайной величины. Для малого числа реализаций оптимального решения имеется риск, что полученный средний результат будет сильно отличаться от математического ожидания соответствующей строки оценочной матрицы.