
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метастратегии и метарасширения
|
|
Смешанные стратегии определяются как случайные величины, реализующиеся в виде чистых стратегий. Дальнейшее расширение понятия стратегии сводится к пониманию новых, обобщенных, стратегий как функций, в которых исходные стратегии принимаются константамиаргументами. В качестве аргументов, которые целесообразно рассматривать для функций от стратегий, можно брать стратегии других игроков [19].
Далее мы ограничимся случаем, когда каждый раз рассматривается функция от стратегии только одного игрока.
Определение 9. В бескоалиционной игре всякая функция Fkij: Xk ® Xj, которая, исходя из стратегии Xk игрока k, определяет стратегию Xj игрока j, называется метастратегией игрока j (в ответ на стратегию игрока k).
Содержательно всякую метастратегию Fkij можно понимать как способ выбора игроком j некоторой своей стратегии в зависимости от получаемой им информации о стратегии, выбираемой игроком k. Если рассматривать ситуацию в бескоалиционной игре как некоторое соглашение (некоторый договор между игроками), а общую стратегию – как принимаемое на себя в договоре обязательство, то метастратегию можно понимать как своего рода условное обязательство: “в случае, если игрок k поступит так-то, я, игрок і, выбираю такую-то свою стратегию, а если этак-то, то такую-то”.
Очевидно, множество всех метастратегий і в ответ на стратегию k можно изобразить в степени множеств  .
.
Определение 10. Бескоалиционные игры G, с тем же множеством игроков N, что и игра G, называется метаигрой над игрой G (метарасширением игры Г), если для некоторых
j, k Î N

и для любой метастратегии yi Î Yi и любого игрока і Î I
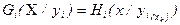 ,
,
где xk – стратегия игрока k, входящая в ситуацию C,
Н – функция выигрышей в игре Г.
Очевидно, процесс образования метаигр (метарасширений игр) поддается неограниченному интегрированию: от метаигры можно переходить к её метаигре (называемой второйметаигрой), от неё – к третьей метаигре и т.д. В этом отношении метарасширения игр отличаются большим разнообразием, чем смешанные расширения.
Для метастратегических расширений доказаны следующие важные теоремы.
Теорема 3. Каждая конечная бескоалиционная игра двух лиц имеет в своём первом метарасширении ситуации равновесия.
Доказанная теорема не противоречит той возможности, что ситуацией равновесия может обладать уже сама исходная игра Г.
Теорема 4. Каждая конечная бескоалиционная игра двух лиц имеет в своем третьем метарасширении ситуацию, которая является одновременно ситуацией равновесия и оптимальной по Паретто.
Пример. Биматричная игра 2´ 2 имеет следующие матрицы выигрышей игроков А и В:

 .
.
В соответствии с выражениями (3.53), (3.54) и (3.55) находим приемлемые ситуации (X, Y) игрока 1:
а) (1, q), где 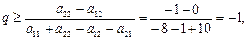
(q может быть в любом интервале [0, 1]);
б) (1, q), где 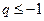 (ситуация невозможна);
(ситуация невозможна);
в) (0, q), где  (ситуация невозможна).
(ситуация невозможна).
В соответствии с выражениями (3.62), (3.63) и (3.64) находим приемлемые ситуации (X, Y) игрока 2:
а) (1, q), где 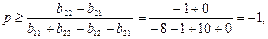
(р может быть любым в интервале [0, 1]);
б) (0, q), где  (ситуация невозможна);
(ситуация невозможна);
в) (p, q), где  (ситуация невозможна);
(ситуация невозможна);
Для наглядности на рис. 3.26 изображены зигзаги, описывающие и невозможные ситуации за пределами допустимых изменений вероятностей p, q.
Единственной ситуацией равновесия в рассматриваемой игре оказывается ситуация (1, 1). В этой ситуации каждый из участников теряет 8. Вместе с тем очевидно, что в ситуации (0, 0) каждый игрок теряет лишь по единице. Однако эта ситуация неустойчива, каждый игрок, изменяя в ней произвольным образом свою стратегию, увеличивает свой выигрыш.

Рис.3.26. Определение ситуации равновесия
Множество всех реализуемых векторов выигрышей для рассматриваемой игры имеет вид, изображенный на рис. 3.27.
Очевидно, что ситуации с выигрышами (–1, –1), (–10, 0), (0, –10) являются оптимальными по Паретто. При этом первая из них, в которой получаются наибольшие выигрыши (–1, –1) для каждого из игроков, лучше, чем равновесная.
Противоречие между осуществимостью ситуации, выражаемой в виде равновесности и её выгодности, которой соответствует оптимальность по Паретто, имеет по существу ту же природу, что и противоречие между максиминным и минмаксным выигрышами. Поэтому оно должно разрешаться при помощи аналогичных приемов, состоящих в расширении уже имеющихся стратегий, т.е. переходу к метарасширениям.

Рис. 3.27. Множество оценок ситуаций биматричной игры
Первая метастратегия игрока 2 состоит в выборе им своей второй стратегии в ответ на вторую стратегию игрока 1 и первой стратегии в ответ на первую.
Вторая метастратегия игрока 1 состоит в выборе им второй своей стратегии, если игрок 2 выберет ту же стратегию, что и 1 и в выборе им своей первой стратегии во всех остальных случаях.
Содержательно это можно представить себе так, что игрок 2 исходит из тезиса “око за око”, а игрок 1 – из более изощренных соображений, которые можно расценить как эгоцентризм (“поддерживать тех, кто действует так же, как я”) и ксенофобию (“выступаю против всех тех, кто действует иначе, чем я”).