Решение игры

В соответствии с выражениями (3.43) и (3.44) приемлемыми ситуациями для игрока 1 будут те, которые удовлетворяют условиям

Рассмотрим три случая:

а) р = 1 (X =|1, 0|). В соответствии с выражением (3.47) имеем

откуда .

б) р = 0 (X =|0, 1|). В соответствии с выражением (3.48) имеем

,

или .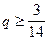

в) 0< р < 1 (X =| р, 1 – р |). В соответствии с выражением (3.49) или в развернутом виде (3.55) получаем

Приемлемые ситуации для игрока 2 в соответствии с выражениями (3.62), (3.63) и (3.64) следующие:

(p, 1), где

(p, 0), где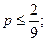

(p, q), где

Множество всех приемлемых ситуаций игрока 1 и игрока 2 изображены на рис. 3.42 25 (для игрока 2 соответствующее множество показано пунктиром).

Рис.3.4225. Множество приемлемых ситуаций для игроков 1 и 2

Зигзаги приемлемых ситуаций пересекаются в единственной точке , которая и оказывается единственной ситуацией равновесия. Эта ситуация равновесия является ситуацией равновесия в смешанных стратегиях. Таким образом, оптимальными стратегиями по Нэшу являются и 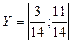. При этом цена игры для игрока 1

.

Цена игры для игрока 2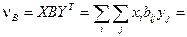

.