Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критерий пессимизма-оптимизма Гурвица. Этот критерий рекомендует при выборе решения не руководствоваться ни крайним пессимизмом (“всегда рассчитывай на худшее!”)
|
|
Этот критерий рекомендует при выборе решения не руководствоваться ни крайним пессимизмом (“всегда рассчитывай на худшее! ”), ни крайним, легкомысленным оптимизмом (“авось, повезет! ”).
Критерий Гурвица охватывает ряд различных подходов к принятию решения: от наиболее оптимистического до наиболее пессимистичного. Согласно этому критерию оптимальная стратегия выбирается из условия
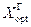= { хk Î Х Ç 
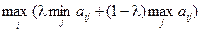}, (4.10)
где l – весовой коэффициент, лежащий в интервале [0; 1];
aij – элементы матрицы прибылей (выигрышей).
При l = 1 критерий Гурвица превращается в критерий Вальда; при l = 0 – в критерий “крайнего оптимизма”. При
0 < l < 1 получается что-то среднее между этими критериями. Коэффициент l выбирается субъектом риска на основании своего опыта, склонности к риску, здравого смысла и т.д. Чем опаснее ситуация, чем больше субъект риска хочет в ней “подстраховаться!, чем меньше его склонность к риску, тем ближе к единице выбирается l. При отсутствии явной склонности к риску, выбор l = 
представляется наиболее разумным.
Пример. Дана матрица прибылей.
| s 1 | s 2 | s 3 | s 4 | |
| Х 1 | ||||
| Х 2 | ||||
| Х 3 | ||||
| Х 4 |
Найти оптимальное решение, используя критерий Гурвица с l =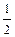 
.
Решение:
;
;
;
.
.
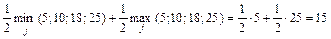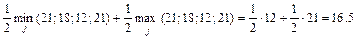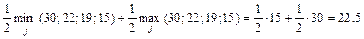Максимальное значение ai обеспечивается применением стратегии х 4.
В случае, если исходная матрица представляет собой матрицу потерь, оптимальная стратегия в соответствии с критерием Гурвица выбирается из условия:
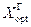= { хk Î Х Ç 
(4.11)
где bij – элементы матрицы потерь (убытков).
Если исходная матрица представляет собой матрицу рисков, то оптимальная стратегия в соответствии с критерием Гурвица выбирается из условия
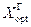= { хk Î Х Ç 
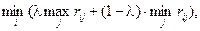(4.12)
где rij – элементы матрицы рисков.
При l = 1, критерий Гурвица превращается в критерий Сэвиджа; при l = 0 – в критерий “крайнего оптимизма” для матрицы рисков.
Пример. Дана матрица потерь.
| s 1 | s 2 | s 3 | s 4 | |
| Х 1 | ||||
| Х 2 | ||||
| х 3 |
Определить оптимальные решения по критерию Гурвица, используя как матрицу потерь, так и соответствующую ей матрицу рисков. Коэффициент l взять равными 1/2.
Решение. Используя соотношение (4.11), в котором вместо величин рисков необходимо подставить потери, получаем
.
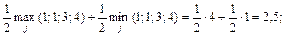
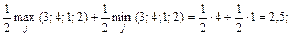
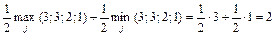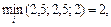
что соответствует выбору стратегии х 3.
Пересчитанная из матрицы потерь матрица рисков имеет вид
| s 1 | s 2 | s 3 | s 4 | |
| Х 1 | ||||
| Х 2 | ||||
| х 3 |
Используя, соотношение (4.12), получаем
.
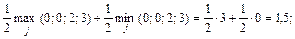
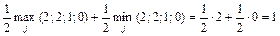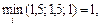что соответствует выбору стратегии х 3.
Можно решить и обратную задачу; для приглянувшегося решения вычислить весовой множитель, который обеспечивает оптимальное решение по критерию Гурвица. Это значение l интерпретируется как показатель риска или соотношения “пессимизма и оптимизма”
Пример. Дана матрица выигрышей
| s1 | s2 | |
| Х 1 | ||
| Х 2 |
Найти решение оптимальное по Гурвицу при l = 0.5. И найти l, при которых это оптимальное решение изменится.
Решение. В соответствии с выражением (4.10) получаем:
a 1 = 0, 5*2 + 0, 5*8 = 5,
a 2 = 0.5*4 + 0, 5*5 = 4, 5.
Тогда ak = max (5; 4, 5) = 5. Следовательно, при l = 0.5 оптимальное решение по критерию Гурвица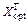 
= х1.
Решим обратную задачу: определим, при каком l, оптимальным по Гурвицу будет решение х 2.
Для того, чтобы оптимальной по Гурвицу было решение х 2, необходимо выполнение неравенства:
l*2 + (1 – l)*8 < l*4 + (1 – l)*5.
Из этого неравенства получаем, что 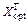= х 2, если
l > 0.6.
Рекомендации. Критерий Гурвица следует применять в случае:
– когда о вероятностях состояния среды ничего неизвестно;
– реализуется лишь малое количество решений;
– допускается некоторый риск.