Критерий Гермейера

Критерий Гермейера является максиминным критерием, который ориентирован на средний наихудший (как правило, отрицательный)результат. В соответствии с этим критерием оптимальное решение выбирается из условия:

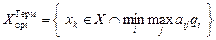. (4.16)

Пример. Два проекта в зависимости от экономической ситуации, которая имеет два состояния, дают доходность, представленную следующей матрицей:

.

Состояния среды имеют следующие вероятности: g ₁ = P (s ₁) = 0, 6;
g ₂ = P (s ₂) = 0, 4.

Определить проект оптимальный по критерию Гермейера.

Решение. В соответствии с (4.16) определяем наихудший средний результат для каждого варианта решений:

a ₁ = 4*0, 4 = 1, 6;

a ₂ = 2*0, 6 = 1, 2;

a_k = max{ a_i } = max{1, 6; 1, 2}=1, 6.

Следовательно, = Х ₁.

Если исходная матрица является матрицей проигрышей | b_ij | или матрицей рисков | r_ij |, оптимальные решения по критерию Гермейера определяются соответственно из условий:

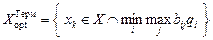. (4.17)

. (4.18)

Критерий Гермейера применяют в следующих случаях:

- имеется информация о вероятностях состояний среды;

- решение реализуется один или несколько раз;

- при малом числе реализаций решения допускается некоторый риск.

Очевидно, что в случае равномерного распределения вероятностей состояний среды, критерий Гермейера совпадает с критерием Вальда.