Принятие решений по критерию Байеса с возможностью проведения эксперимента

Пусть ЛПР известны вероятности различных состояний среды 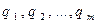и матрица выигрышей .

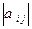Если эксперимент не проводится, то в соответствии с критерием Байеса, выбирается то решение 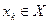, которое обеспечивает максимальный средний выигрыш:

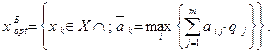
Предположим, что у ЛПР имеется возможность проведения эксперимента (поиска дополнительной информации) с целью уточнения состояния среды, затраты на который составляют величину .

Эксперимент называется идеальным, если по его результатам будущее состояние среды определяется точно.

Пусть эксперимент проведён и выяснено состояние среды, которое действительно состоится. Зная это состояние среды, ЛПР, конечно, будет выбирать то решение, которое обеспечивает ему максимальный выигрыш при данном состоянии среды. Если этим состоянием среды оказалось , то оптимальное решение обеспечит выигрыш:

Так как вероятность того, что среда окажется в состоянии равна , то результат идеального эксперимента (до его проведения) является случайной величиной, со следующим рядом распределения вероятностей:

Математическое ожидание этого гипотетического выигрыша равно

Вычитая от стоимость эксперимента, находим итоговый средний выигрыш

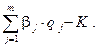
Идеальный эксперимент следует проводить, если

(4.19)

Перепишем неравенство (4.19) в следующем виде:

(4.20)

Так как для каждой матрицы , то соотношение (4.20) можно записать в виде

(4.21)

Учитывая, что – это риск, окончательно получаем

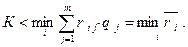(4.22)

Величина является максимально допустимой стоимостью идеального i -го эксперимента. Таким образом, если затраты на проведение эксперимента (добывание информации) меньше минимального среднего риска, то его следует проводить.

Пример. Матрица выигрышей 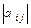имеет вид:

,

где имеет размерность тыс. грн..

Вектор вероятностей состояний среды 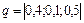. Стоит ли проводить идеальный эксперимент, если его стоимость составляет 1 тыс. грн?

Решение. От матрицы выигрышей переходим к матрице рисков:

.

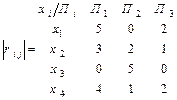Определяем средние риски для каждого решения:

Так как 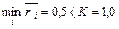, то эксперимент проводить нецелесообразно. В качестве оптимального решения следует выбирать решение х ₃, для которой средний риск минимален. Этой стратегии всегда будет соответствовать и максимальный средний выигрыш.

Рассмотрим случай неидеального эксперимента, когда его результат не позволяет точно определить будущее состояние среды, а лишь приводит к одному из несовместимых исходов 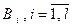. Каждый из этих исходов даст лишь вероятностные данные относительно тех или иных состояний среды . Предлагается, что условные вероятности 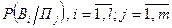, появления событий (исходов эксперимента) при условии, что состояние среды соответствует , известны.

Пусть в результате проведённого эксперимента получен исход . Тогда используя формулу Байеса, можно определить апостериорные вероятности состояний среды:

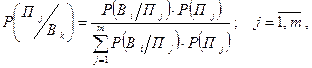
где 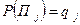– априорная вероятность гипотезы, что состояние среды соответствует .

Используя апостериорные вероятности состояний среды, находим апостериорные средние выигрыши:

Оптимальная стратегия при k -ом исходе соответствует максимальному апостериорному среднему выигрышу .

Решение о целесообразности проведения неидеального эксперимента производится на основе выполнения неравенства:

(4.23)

где вероятность исходов определяется по формуле полной вероятности:

(4.24)

Если неравенство (4.23) выполняется, то проведение эксперимента целесообразно, в противном случае – нецелесообразно.

Пример. Матрица выигрышей (в тыс. грн.) для случая неопределённости состояний среды имеет вид:

.

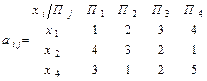Априорные вероятности состояний среды равны Стоимость неидеального эксперимента, уточняющего состояние среды, равна 600 грн..

Определить целесообразность проведения эксперимента, если он приводит к двум исходам В ₁ и В ₂, а условные вероятности приведены в следующей таблице:

_.

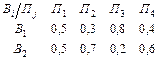Решение.

1. Определяем максимальный априорный средний выигрыш:

Следовательно, если эксперимент не проводить то оптимальной по критерию Байеса является решение , которой соответствует средний выигрыш 2, 6.

Определяем:

1. вероятности исходов экспериментов

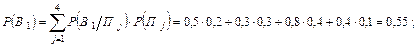
2. Определяем апостериорные вероятности состояний среды для каждого из исходов неидеального эксперимента. Если исход эксперимента ₁, то:

Если имел место исход , тот апостериорные вероятности равны:

3. Находим максимальный средний апостериорный выигрыш для каждого из исходов :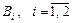

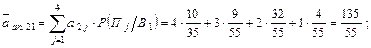
Таким образом, если бы результатом эксперимента был исход , то оптимальным решением было бы решение , при котором средний апостериорный выигрыш максимален и равен .

Определяем средние апостериорные выигрыши для каждого решения при исходе :

Если бы в результате эксперимента получился исход , то оптимальным решением было бы решение , обеспечивающее средний апостериорный выигрыш .

Для определения целесообразности проведения неидеального эксперимента в соответствии с (4.23) рассчитываем величину:

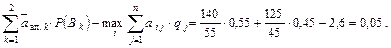
Так как то эксперимент проводить нецелесообразно, а решение следует принимать по критерию Байеса. Используя априорные вероятности .

Итак, при принятии решения по критерию Байеса с возможностью проведения эксперимента ЛПР принимает вначале решение проводить ли эксперимент, а затем выбирает оптимальное решение в зависимости от результата эксперимента (если была принято решение его проводить) или на основании априорных вероятностей состояния среды (если было принято решение эксперимент не проводить).

Данная многошаговая задача принятия решений может быть представлена в виде дерева игры и решаться как позиционная игра, в которой в роли второго игрока выступает среда.