Многокритериальные решения, оптимальные по Парето

Математическая модель многокритериальной задачи принятия решений (ЗПР) может быть представлена в виде матрицы F (х) размером (n * m), элементами которой являются оценки f_j (х_i) отдельных (частных) критериев f_j (х), 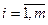, которые подлежат либо максимизации, либо минимизации на всем множестве возможных решений X = (x ₁, x ₂, …, x_n). Требуется найти такое x_i, которое дает наилучший результат по этим критериям. Отметим, что критерий, подлежащий максимизации, можно всегда преобразовать в критерий, подлежащий минимизации (или наоборот), путем изменения знака f_j (х) (рис. 5.1).

Рис.5.1. Преобразование задачи максимизации в задачу минимизации

Далее, если это не будет оговорено, будем предполагать, что все критерии подлежат максимизации.

Идеальным в данной задаче является нахождение такого решения х_а, называемого абсолютным, которое является наилучшим по всем критериям, т.е. принадлежит пересечению множеств решений всех однокритериальных задач:

. (5.1)

Обычно это множество пусто (решение х_а не существует), и тогда вначале ищут решения, оптимальные по Парето. В теории многокритериальной оптимизации их еще называют эффективными [12].

Определение. Решения х ^* называются оптимальными по Парето, если для любых других х Î Х имеет место неравенство

, (5.2)

причем хотя бы для одного индекса j имеет место строгое неравенство.

Очевидно, что в задаче минимизации всех частных критериев знак неравенства в (5.2) нужно изменить на противоположный.

Определение. Решение х_i доминирует по Парето решение х_j (записывается в виде ), если векторная оценка этого решения (f ₁(x_i)), (f ₂(x_i)), …, (f_m (x_i)) превосходит векторную оценку решения х_j (f ₁(x_j)), (f ₂(x_j)), …, (f_m (x_j)), т.е. для случая максимизации всех критериев выполняется условие

, (5.3)

причем, по крайней мере, для одного из е неравенство выполняется строго.

Для случая минимизации всех критериев знак неравенства в (5.3) необходимо поменять на противоположный.

Очевидно, что одни Парето-оптимальные решения не могут доминировать другие Парето-оптимальные решения.

Таким образом, алгоритм нахождения оптимальных по Парето решений заключается в исключении решений, которые не доминируют по Парето другие решения.

Пример. Найти решения, оптимальные по Парето, для следующих исходных данных (все критерии f_j (x)) подлежат минимизации):

Неравенство (5.2) означает, что Парето-оптимальные решения заведомо лучше остальных решений. Поэтому, чтобы найти их, необходимо исключить из множества Х заведомо худшие решения. Оставшиеся решения и будут Парето-оптимальными.

В рассмотренной задаче решение х ₃ заведомо худшее, чем х ₄, поскольку по первому и третьему критериям оно имеет большие значения (имеет место строгое неравенство в (5.2)), а по второму критерию оценки равны. Из оставшихся х ₁, х ₂, х ₄ решений никакое исключать нельзя, т.к. по одному критерию лучше одно решение, а по другому – другое.

Ответ. Оптимальными по Парето являются решения х ₁, х ₂, х ₄.

В общем случае Парето-оптимальных решений несколько (решение не однозначно), но эти решения не эквивалентны между собой. В этом легко убедиться на следующем примере:

В этом примере оба решения оптимальны по Парето, но второе решение х ₂ по четырем критериям лучше первого критерия х ₁.

Рассмотрим еще один пример определения оптимальных по Парето решений.

Пример. Найти решение двухкритериальной задачи, в которой оба критерия f ₁(х) и f ₂(x) необходимо максимизировать. Пусть множество решений Х и область их оценок представлены так, как показано на рис. 5.2.

Рис. 5.2. Нахождение Парето-оптимальных решений

На рис.5.2 множеству Парето-оптимальных решений соответствует дуга АСВ. Действительно, любое решение х, имеющее оценки критериев, лежащих не на дуге АСВ, может быть улучшено, хотя бы по одному критерию, при этом не ухудшено по другому критерию. Если же иметь решение, соответствующее любой точке дуги АСВ, то при переходе к другой точке этой же дуги значение по одному из критериев ухудшится.

Если оба критерия необходимо минимизировать, то множеству Парето будет соответствовать дуга DKL.

Пример. Пусть в двухкритериальной задаче критерий f ₁(x) необходимо максимизировать, а f ₂(x) – минимизировать. На рис. 5.3 показаны оценки по этим критериям для всех десяти возможных решений. Необходимо найти из этих решений Парето-оптимальные.

Рис. 5.3.Нахождение Парето-оптимальных решений

Решение. Исключаем решения, которые не доминируют по Парето, т.е. такие решения, от которых можно перейти к другим, у которых оценки по всем критериям будут не хуже, а хотя бы по одному критерию лучше.

Очевидно, что решение х ₅ надо исключить, поскольку решение х ₂ имеет большее значение f ₁(x) и меньшее значение f ₂(x). Также исключаются решения х ₄, х ₇, х ₈, х ₃, х ₁. Остаются только решения х ₉, х ₁₀, х ₂, х ₆, которые и являются Парето-оптимальными. Действительно, если, например, перейти от решения х ₁₀ к решению х ₂, то значение критерия f ₂(x) ухудшится.

Дать однозначный ответ, какое из нескольких Парето-оптимальных решений считать наилучшим невозможно без дополнительной информации, например о приоритетности критериев. Но “кандидатом” на это наилучшее решение может быть только решение из множества Парето-оптимальных. Поэтому нахождение Парето-оптимальных решений уменьшает количество решений, из которых ЛПР должно выбрать единственное. Для нахождения единственного оптимального решения необходимо частные критерии f_j (x) каким-то образом “свернуть” в один обобщенный скалярный критерий. Под обобщенным критерием в многокритериальной задаче принятия решений понимается такая скалярная функция f (x), которая превращает векторную оценку решения в скалярную.

Перед сверткой критериев необходимо решить задачу определения приоритетности критериев и задачу нормализации значений частных критериев.