Аддитивный обобщенный критерий

Наиболее распространенным обобщенным критерием является “взвешенная” сумма частных критериев

, (5.7)

где k_i > 0, 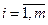- коэффициенты приоритетности критериев (весовые коэффициенты), которые удовлетворяют условию .

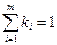Если размерность частных критериев различна, то ,

где f_{j н}(x) – нормированные частные критерии.

Очевидно, что чем больше k_j, тем больший вклад j -го критерия в обобщенный показатель независимо от того, подлежит ли частный критерий максимизации или минимизации.

Легко показать, что решение x Î X, оптимальное по обобщенному аддитивному критерию, является и Парето-оптимальным в множестве возможных решений Х.

Пример. Найти оптимальное решение, используя обобщенный аддитивный критерий, для следующей многокритериальной задачи:

Первый критерий предпочтительнее второго, а второй – третьего. Все критерии подлежат максимизации. Размерности оценок решений по всем критериям одинаковы.

Решение. Коэффициенты приоритетности найдем, используя формулу Фишберна:

.

Поскольку размерности оценок по всем критериям одинаковы, нормализацию в данной задаче не проводим.

Используя обобщенный аддитивный критерий , получаем

Так как 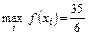, то х _opt = х _1.

Если бы приоритетность критериев была одинаковой (k ₁ = k ₂ = k ₃ = 1/3), то оптимальным решением было бы х _4.

Но ни при каких коэффициентах приоритетности решение х ₅ не станет оптимальным, поскольку оно не является Парето-оптимальным: x ₁ > x ₅. Поэтому решение х ₅ можно было бы сразу исключить из дальнейшего рассмотрения.

Главным недостатком обобщенного аддитивного критерия является то, что при его применении может происходить взаимная компенсация частных критериев: уменьшение одного из показателей может быть компенсировано возрастанием другого.