Неоднозначность оптимальных решений по аддитивному и мультипликативному обобщенным критериям

Пусть каждое решение оценивается двумя критериями: результатом (этот критерий нужно максимизировать) и затратами (этот критерий необходимо минимизировать). Предположим, что оба критерия имеют одну и ту же единицу размерности, поэтому нормализацию проводить не требуется.

Тогда обобщенный аддитивный критерий имеет вид

, (5.8)

где – коэффициенты приоритетности результата решения и затрат на его исполнение соответственно.

Обобщенный мультипликативный критерий

. (5.9)

Оказывается, решения, принимаемые по этим обобщенным критериям, совпадают не всегда [23].

Определим ситуации, когда решения по этим критериям совпадают и когда не совпадают.

Пусть . Тогда очевидно, что решение x ₁ предпочтительнее решения x ₂ по обоим обобщенным критериям, если , и, наоборот, x ₁ хуже решения x ₂ по обоим критериям, если .

Пусть 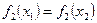. Тогда, если , решение x ₁ предпочтительнее x ₂, а если , предпочтительным является решение x ₂. Также тривиальным является случай, когда одно решение лучше другого, как по результату, так и по затратам. Например, если и , то по обоим обобщенным критериям лучшим является решение x ₁.

Рассмотрим нетривиальный случай

; (5.10)

. (5.11)

Введем положительные числа a > 0 и b > 0 такие, что

; (5.12)

. (5.13)

Тогда значение обобщенного аддитивного критерия для решения x ₁ равно

, (5.14)

а для решения x ₂ с учетом выражений (5.12), (5.13) имеем

Очевидно, что решение x ₁ будет предпочтительнее решения x ₂ в случае

. (5.15)

Итак, получаем, что если использовать обобщенный аддитивный критерий, то для условий (5.10), (5.11) оптимальное решение удовлетворяет условиям:

. (5.16)

В выражении (5.16) знак «>» означает, что первое решение лучше второго; знак «<» – что первое решение хуже второго; знак «º» – оба решения равноценны.

Как видим, условия (5.16) зависят как от соотношения , так и от соотношения коэффициентов приоритетности .

Рассмотрим задачу принятия решения при использовании обобщенного мультипликативного критерия:

; (5.17)

(5.18)

Решение x ₁ будет предпочтительнее решения x ₂, если

, или . (5.19)

Раскрывая неравенство (5.19) и учитывая, что ; , получаем, что при использовании обобщенного мультипликативного критерия оптимальные решения удовлетворяют следующим условиям:

. (5.20)

Условия (5.20) определяются только соотношением и не зависят от соотношения коэффициентов приоритетности.

Условия (5.16) и (5.20) одновременно представим в прямоугольной системе координат (рис.5.4).

Рис. 5.4. Области, определяющие однозначность и неоднозначность принятия решения при использовании аддитивного и мультипликативного критериев

Как видно из рис.5.4, области II и IV соответствуют различным оптимальным решениям, если использовать различные обобщенные критерии, а области I и III обеспечивают одно и то же оптимальное решение.

Область II соответствует условиям

; (5.21)

. (5.22)

Пример. Пусть ; ; a = 2; b = 3; f ₁(x ₁) = 4 ден. ед.; f ₂(x ₁) = 3, 5 ден. ед. Требуется найти оптимальное решение по обобщенному аддитивному и мультипликативному критериям.

Решение. Так как f ₁(x ₂) = f ₁(x ₁) - a = 4 - 2 = 2; f ₂(x ₂) = f ₂(x ₁) - b = 3, 5 - 3 = 0, 5, то

;

.

Так как , то решение x ₁ является оптимальным, если использовать обобщенный аддитивный критерий.

Найдем решение по мультипликативному критерию.

;

.

Так как 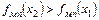, то решение x ₂ лучше решения x ₁.

Таким образом, получили по разным обобщенным критериям разные решения, поскольку начальные условия данной задачи соответствуют области II. Действительно, ; , а следовательно, условия (5.21) и (5.22) выполняются.

Область противоположных решений IV соответствует условиям

; (5.23)

. (5.24)

Покажем, что условия (5.23) и (5.24) не всегда могут удовлетворять реальным решениям, у которых , то есть результат выше затрат. Действительно, если k ₁ > k ₂, то , то есть b > a. Но в этом случае, чтобы выполнить условие (5.24), необходимо, чтобы f ₂(x ₁) было больше f ₁(x ₁) (затраты должны быть выше результата).

Если же k ₁ < k ₂, то может быть меньше единицы (если ), а в этом случае условие (5.24) может быть выполнено и при .

Пример. Пусть ; ; a = 1; b = 0, 5; f ₁(x ₁) = 5; f ₂(x ₁) = 3. Эти начальные условия удовлетворяют области IV.

Действительно, ; .

Найдем для данных условий решения, оптимальные по обобщенному аддитивному и мультипликативному критериям.

f ₁(x ₂) = f ₁(x ₁) - a = 5 - 1 = 4; f ₂(x ₂) = f ₂(x ₁) - b = 3 - 0, 5 = 2, 5;

;

.

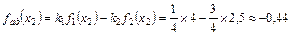Так как , то решение x ₂ является оптимальным по аддитивному критерию.

;

.

Так как , то по мультипликативному критерию предпочтительным является решение x ₁.

При выполнении условий

; ; (5.25)

; (5.26)

оптимальные решения по обобщенным аддитивному и мультипликативному критериям совпадают.